
| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |

|
|
Program file for this chapter: fsm
As I explained in the preface to the first volume, one of my purposes in writing this series of books has been to urge computer hobbyists away from the view of computer expertise as the knowledge of obscure characteristics of some particular computer--how to program it in machine language, what magic numbers can be found where in its memory, how to overcome the copy protection schemes on its disks, and so on. The trouble with this sort of machine-specific expertise is that it becomes obsolete when your favorite computer does. From my point of view, one of the virtues of Logo as a programming language is that its high level data structures direct your attention away from questions about what goes where in memory, allowing you to focus instead on a more abstract description of your problem.
Automata theory is a further step in abstracting your attention away from any particular kind of computer or particular programming language. In automata theory we consider a mathematical model of computing. Such a model strips the computational machinery--the "programming language"--down to the bare minimum, so that it's easy to manipulate these theoretical machines (there are several such models, for different purposes, as you'll soon see) mathematically to prove things about their capabilities. For the most part, these mathematical models are not used for practical programming problems. Real programming languages are much more convenient to use. But the very flexibility that makes real languages easier to use also makes them harder to talk about in a formal way. The stripped-down theoretical machines are designed to be examined mathematically.
What's a mathematical model? You'll see one shortly, called a "finite-state machine."
The point of this study is that the mathematical models are, in some important ways, equivalent to real computers and real programming languages. What this means is that any problem that can be solved on a real computer can be solved using these models, and vice versa. Anything we can prove about the models sheds light on the real problems of computer programming as well.
The questions asked in automata theory include these: Are there any problems that no computer can solve, no matter how much time and memory it has? Is it possible to prove that a particular computer program will actually solve a particular problem? If a computer can use two different external storage devices (disks or tapes) at the same time, does that extend the range of problems it can solve compared to a machine with only one such device?
There is also a larger question lurking in the background of automata theory: Does the human mind solve problems in the same way that a computer does? Are people subject to the same limitations as computers? Automata theory does not actually answer this question, but the insights of automata theory can be helpful in trying to work out an answer. We'll have more to say about this in the chapter on artificial intelligence.
What kinds of problems can we give to our abstract computers? In automata theory we want to focus our attention on computation itself, not on details of input and output devices. So we won't try creating a mathematical model of a video game.
We will play a game, though. In this game the computer has a rule in mind.
You type in strings of letters, using only the letters A, B, and
C. The computer tells you whether each string follows the rule or
not. Your job is to guess the rule. For example, suppose you have done
these experiments:
| accepted | rejected |
|---|---|
ABC | CBA
|
AAA | BBB
|
ABCABCABC | BCABCABC
|
A | BBBBBBB
|
ACCCCCCCCC | CAAAAAAAAA
|
You might guess, from these examples, that the rule is
"The string must begin with A." Once you've made a guess you can
test it out by trying more examples.
The program to play the game is called game. It takes one input,
a number from 1 to 10. I've provided ten different rules. Rules 1 to 3
should be pretty easy to guess; rules 8 to 10 should be nearly impossible.
(Don't feel too frustrated if you don't get them.)
A string can be any length, including length zero (the empty string). Each
time you type a letter the program lets you know whether the string you've
typed so far obeys the rule. The program indicates whether the string is
accepted or rejected by displaying the word accept or reject on
the screen. In particular, as soon
as you start game the program will tell you whether or not the empty
string is accepted by this rule. If you type the string ABC you'll
really be testing three strings: A, AB, and ABC. You
should type one letter at a time to make sure the program has a chance to
respond to it before going on to the next letter. To start over again with
a different string, press the Return key.
You should stop reading now and try the game. In the following paragraphs I'm going to talk about some of the answers, so this is your last chance. After you've figured out at least some of the rules, come back to the book.
The point of studying this game is that we're going to look at a way to design a special-purpose abstract computer that understands one particular rule. We can then ask questions about how much information the computer needs to handle the job.
You've seen the word state before in connection with the Logo
turtle. Its state includes its position and its heading. So one turtle
state might be "position [17 82], heading 90." In principle,
the turtle has an infinite number of possible states, because its
position and heading don't have to be integers. Its position might be
[14.142 14.142], for instance.
Anything that holds information can be in different states. As another example, an on-off light switch has two states. Some lamps have four states: off, low, medium, and high. A computer, too, has a certain number of states. The state of a computer includes all the information in its memory at some particular time.
A machine that has only a limited number of states, like the example of the light switch, is called a finite-state machine. For almost all of this chapter we'll be dealing with finite-state machines. You might think that that imposes a very severe limit on the kinds of computations we can do. But note that in the game I asked you to play, a rule can accept an infinite number of possible strings and reject an infinite number of others. The accepted or rejected strings can be of any length. (Some rules restrict the length of a string, but others allow any length at all.) In some sense, a finite-state machine can still perform infinitely varied computations.
Consider the third game as an example. The rule is "Accept
any string that starts with AB." Here is a picture of a finite-state
machine that implements that rule:
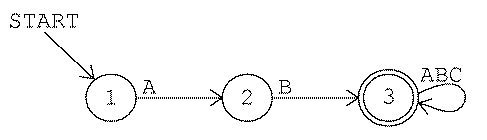
Each numbered circle represents a state. This machine has three
states. The start arrow indicates that the machine starts out in state
1. State 3 is shown with a double circle to indicate that it is an
accepting state. In other words, when the machine is in state 3 the
screen says accept. The other two states are not
accepting states.
Every time you type a character the machine switches from one state to
another. The arrow from state 1 to state 2 has an A next to its
tail. This indicates that when the machine is in state 1, an input of
A switches it to state 2. (The arrow from state 3 to itself has the
three letters ABC at its tail. This is a shorthand notation for
three separate arrows with heads and tails in the same place, one for each
letter.)
This picture is actually incomplete. For a full description of the machine
we have to indicate what happens on any input in any state. In other words,
each circle should have three arrows coming out from it, one each
for A, B, and C. I've chosen to adopt the convention that
every machine has an unmarked state called reject. Any missing arrow
goes to that state; once the machine is in the reject state it stays
there forever. Here, then, is the complete diagram of the machine for game
3:

From now on I won't draw the reject state, but you should
remember that it's really part of the machine description. So this machine
requires four states, not three.
If the first input letter isn't A, the machine goes to the reject
state. If the first letter is A, the machine goes to state 2. Then,
if the second letter is B, the machine ends up in state 3 and accepts
the string AB. This is the shortest acceptable string.
Each of the three arrows from state 3 loops right back into state
3 itself. (Remember, although only one arrow appears in the picture,
it is labeled with three letters, so officially it represents three
arrows.) This means that once the machine is in state 3 it stays
there no matter what inputs it gets. Any string that starts AB is
acceptable.
Here is a machine for game number 2:

In this machine the start state is also an accepting
state. (Every machine has exactly one start state, but it may have any
number of accepting states.) This machine never gets into the reject
state. That doesn't mean it doesn't reject any strings; all odd-length
strings are rejected in state 2. But a rejected string can redeem itself by
adding another input character, so state 2 allows a return to the accepting
state 1.
Here is a machine for game number 5. (Notice that I'm saying "a machine" and not "the machine"; it is always possible to design other machines that would follow the same rule.)

You probably had more trouble discovering rule 5 than rule
2, and it takes longer to say the rule in English words. But the
machines for the two rules are almost identical. (Remember,
though, that the rule-5 machine really has a third state, the reject
state, which is not shown in the diagram.)
Here are machines for rules 7 and 9. With these machines as hints,
can you figure out the rules? Go back to the game program to test
your hypotheses.

You should also get some practice translating in the other direction, from
English rules to machine diagrams. Here are a couple to work on: Rule 4 is
"To be accepted a string must be composed of doubled letters (AA,
/*
* (C)opyright MMVI Anselm R. Garbe <garbeam at gmail dot com>
* See LICENSE file for license details.
*/
#include "dwm.h"
#include <errno.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <unistd.h>
#include <sys/select.h>
#include <X11/cursorfont.h>
#include <X11/keysym.h>
#include <X11/Xatom.h>
#include <X11/Xproto.h>
/* extern */
char stext[1024];
Bool *seltag;
int bx, by, bw, bh, bmw, master, screen, sx, sy, sw, sh;
unsigned int ntags, numlockmask;
Atom wmatom[WMLast], netatom[NetLast];
Bool running = True;
Bool issel = True;
Client *clients = NULL;
Client *sel = NULL;
Client *stack = NULL;
Cursor cursor[CurLast];
Display *dpy;
DC dc = {0};
Window root, barwin;
/* static */
static int (*xerrorxlib)(Display *, XErrorEvent *);
static Bool otherwm, readin;
static void
cleanup(void) {
close(STDIN_FILENO);
while(sel) {
resize(sel, True, TopLeft);
unmanage(sel);
}
if(dc.font.set)
XFreeFontSet(dpy, dc.font.set);
else
XFreeFont(dpy, dc.font.xfont);
XUngrabKey(dpy, AnyKey, AnyModifier, root);
XFreePixmap(dpy, dc.drawable);
XFreeGC(dpy, dc.gc);
XDestroyWindow(dpy, barwin);
XSetInputFocus(dpy, PointerRoot, RevertToPointerRoot, CurrentTime);
XSync(dpy, False);
free(seltag);
}
static void
scan(void) {
unsigned int i, num;
Window *wins, d1, d2;
XWindowAttributes wa;
wins = NULL;
if(XQueryTree(dpy, root, &d1, &d2, &wins, &num)) {
for(i = 0; i < num; i++) {
if(!XGetWindowAttributes(dpy, wins[i], &wa))
continue;
if(wa.override_redirect || XGetTransientForHint(dpy, wins[i], &d1))
continue;
if(wa.map_state == IsViewable)
manage(wins[i], &wa);
}
}
if(wins)
XFree(wins);
}
static void
setup(void) {
int i, j;
unsigned int mask;
Window w;
XModifierKeymap *modmap;
XSetWindowAttributes wa;
/* init atoms */
wmatom[WMProtocols] = XInternAtom(dpy, "WM_PROTOCOLS", False);
wmatom[WMDelete] = XInternAtom(dpy, "WM_DELETE_WINDOW", False);
netatom[NetSupported] = XInternAtom(dpy, "_NET_SUPPORTED", False);
netatom[NetWMName] = XInternAtom(dpy, "_NET_WM_NAME", False);
XChangeProperty(dpy, root, netatom[NetSupported], XA_ATOM, 32,
PropModeReplace, (unsigned char *) netatom, NetLast);
/* init cursors */
cursor[CurNormal] = XCreateFontCursor(dpy, XC_left_ptr);
cursor[CurResize] = XCreateFontCursor(dpy, XC_sizing);
cursor[CurMove] = XCreateFontCursor(dpy, XC_fleur);
modmap = XGetModifierMapping(dpy);
for (i = 0; i < 8; i++) {
for (j = 0; j < modmap->max_keypermod; j++) {
if(modmap->modifiermap[i * modmap->max_keypermod + j] == XKeysymToKeycode(dpy, XK_Num_Lock))
numlockmask = (1 << i);
}
}
XFree(modmap);
wa.event_mask = SubstructureRedirectMask | SubstructureNotifyMask
| EnterWindowMask | LeaveWindowMask;
wa.cursor = cursor[CurNormal];
XChangeWindowAttributes(dpy, root, CWEventMask | CWCursor, &wa);
grabkeys();
initrregs();
for(ntags = 0; tags[ntags]; ntags++);
seltag = emallocz(sizeof(Bool) * ntags);
seltag[0] = True;
/* style */
dc.norm[ColBG] = getcolor(NORMBGCOLOR);
dc.norm[ColFG] = getcolor(NORMFGCOLOR);
dc.sel[ColBG] = getcolor(SELBGCOLOR);
dc.sel[ColFG] = getcolor(SELFGCOLOR);
dc.status[ColBG] = getcolor(STATUSBGCOLOR);
dc.status[ColFG] = getcolor(STATUSFGCOLOR);
setfont(FONT);
bmw = textw(FLOATSYMBOL) > textw(TILESYMBOL) ? textw(FLOATSYMBOL) : textw(TILESYMBOL);
sx = sy = 0;
sw = DisplayWidth(dpy, screen);
sh = DisplayHeight(dpy, screen);
updatemaster();
bx = by = 0;
bw = sw;
dc.h = bh = dc.font.height + 2;
wa.override_redirect = 1;
wa.background_pixmap = ParentRelative;
wa.event_mask = ButtonPressMask | ExposureMask;
barwin = XCreateWindow(dpy, root, bx, by, bw, bh, 0, DefaultDepth(dpy, screen),
CopyFromParent, DefaultVisual(dpy, screen),
CWOverrideRedirect | CWBackPixmap | CWEventMask, &wa);
XDefineCursor(dpy, barwin, cursor[CurNormal]);
XMapRaised(dpy, barwin);
dc.drawable = XCreatePixmap(dpy, root, sw, bh, DefaultDepth(dpy, screen));
dc.gc = XCreateGC(dpy, root, 0, 0);
XSetLineAttributes(dpy, dc.gc, 1, LineSolid, CapButt, JoinMiter);
issel = XQueryPointer(dpy, root, &w, &w, &i, &i, &i, &i, &mask);
strcpy(stext, "dwm-"VERSION);
}
/*
* Startup Error handler to check if another window manager
* is already running.
*/
static int
xerrorstart(Display *dsply, XErrorEvent *ee) {
otherwm = True;
return -1;
}
/* extern */
int
getproto(Window w) {
int i, format, protos, status;
unsigned long extra, res;
Atom *protocols, real;
protos = 0;
status = XGetWindowProperty(dpy, w, wmatom[WMProtocols], 0L, 20L, False,
XA_ATOM, &real, &format, &res, &extra, (unsigned char **)&protocols);
if(status != Success || protocols == 0)
return protos;
for(i = 0; i < res; i++)
if(protocols[i] == wmatom[WMDelete])
protos |= PROTODELWIN;
free(protocols);
return protos;
}
void
sendevent(Window w, Atom a, long value) {
XEvent e;
e.type = ClientMessage;
e.xclient.window = w;
e.xclient.message_type = a;
e.xclient.format = 32;
e.xclient.data.l[0] = value;
e.xclient.data.l[1] = CurrentTime;
XSendEvent(dpy, w, False, NoEventMask, &e);
XSync(dpy, False);
}
void
quit(Arg *arg) {
readin = running = False;
}
/*
* There's no way to check accesses to destroyed windows, thus those cases are
* ignored (especially on UnmapNotify's). Other types of errors call Xlibs
* default error handler, which may call exit.
*/
int
xerror(Display *dpy, XErrorEvent *ee) {
if(ee->error_code == BadWindow
|| (ee->request_code == X_SetInputFocus && ee->error_code == BadMatch)
|| (ee->request_code == X_PolyText8 && ee->error_code == BadDrawable)
|| (ee->request_code == X_PolyFillRectangle && ee->error_code == BadDrawable)
|| (ee->request_code == X_PolySegment && ee->error_code == BadDrawable)
|| (ee->request_code == X_ConfigureWindow && ee->error_code == BadMatch)
|| (ee->request_code == X_GrabKey && ee->error_code == BadAccess)
|| (ee->request_code == X_CopyArea && ee->error_code == BadDrawable))
return 0;
fprintf(stderr, "dwm: fatal error: request code=%d, error code=%d\n",
ee->request_code, ee->error_code);
return xerrorxlib(dpy, ee); /* may call exit */
}
int
main(int argc, char *argv[]) {
int r, xfd;
fd_set rd;
if(argc == 2 && !strncmp("-v", argv[1], 3)) {
fputs("dwm-"VERSION", (C)opyright MMVI Anselm R. Garbe\n", stdout);
exit(EXIT_SUCCESS);
}
else if(argc != 1)
eprint("usage: dwm [-v]\n");
dpy = XOpenDisplay(0);
if(!dpy)
eprint("dwm: cannot open display\n");
xfd = ConnectionNumber(dpy);
screen = DefaultScreen(dpy);
root = RootWindow(dpy, screen);
otherwm = False;
XSetErrorHandler(xerrorstart);
/* this causes an error if some other window manager is running */
XSelectInput(dpy, root, SubstructureRedirectMask);
XSync(dpy, False);
if(otherwm)
eprint("dwm: another window manager is already running\n");
XSync(dpy, False);
XSetErrorHandler(NULL);
xerrorxlib = XSetErrorHandler(xerror);
XSync(dpy, False);
setup();
drawstatus();
scan();
/* main event loop, also reads status text from stdin */
XSync(dpy, False);
procevent();
readin = True;
while(running) {
FD_ZERO(&rd);
if(readin)
FD_SET(STDIN_FILENO, &rd);
FD_SET(xfd, &rd);
r = select(xfd + 1, &rd, NULL, NULL, NULL);
if((r == -1) && (errno == EINTR))
continue;
if(r > 0) {
if(readin && FD_ISSET(STDIN_FILENO, &rd)) {
readin = NULL != fgets(stext, sizeof(stext), stdin);
if(readin)
stext[strlen(stext) - 1] = 0;
else
strcpy(stext, "broken pipe");
drawstatus();
}
}
else if(r < 0)
eprint("select failed\n");
procevent();
}
cleanup();
XCloseDisplay(dpy);
return 0;
}