


|
|
Suppose we're using Scheme to model an ice cream shop. We'll certainly need to know all the flavors that are available:
(vanilla ginger strawberry lychee raspberry mocha)
For example, here's a procedure that models the behavior of the salesperson when you place an order:
(define (order flavor)
(if (member? flavor
'(vanilla ginger strawberry lychee raspberry mocha))
'(coming right up!)
(se '(sorry we have no) flavor)))
But what happens if we want to sell a flavor like "root beer fudge ripple" or "ultra chocolate"? We can't just put those words into a sentence of flavors, or our program will think that each word is a separate flavor. Beer ice cream doesn't sound very appealing.
What we need is a way to express a collection of items, each of which is itself a collection, like this:
(vanilla (ultra chocolate) (heath bar crunch) ginger (cherry garcia))
This is meant to represent five flavors, two of which are named by single words, and the other three of which are named by sentences.
Luckily for us, Scheme provides exactly this capability. The data structure
we're using in this example is called a list. The difference
between a sentence and a list is that the elements of a sentence must be
words, whereas the elements of a list can be anything at all: words, #t, procedures, or other lists. (A list that's an element of another list
is called a sublist. We'll use the name structured
list for a list that includes sublists.)
Another way to think about the difference between sentences and lists is that the definition of "list" is self-referential, because a list can include lists as elements. The definition of "sentence" is not self-referential, because the elements of a sentence must be words. We'll see that the self-referential nature of recursive procedures is vitally important in coping with lists.
Another example in which lists could be helpful is the pattern matcher. We
used sentences to hold known-values databases, such as this one:
(FRONT YOUR MOTHER ! BACK SHOULD KNOW !)
This would be both easier for you to read and easier for programs to manipulate if we used list structure to indicate the grouping instead of exclamation points:
((FRONT (YOUR MOTHER)) (BACK (SHOULD KNOW)))
We remarked when we introduced sentences that they're a feature we added to Scheme just for the sake of this book. Lists, by contrast, are at the core of what Lisp has been about from its beginning. (In fact the name "Lisp" stands for "LISt Processing.")
When we introduced words and sentences we had to provide ways to take them
apart, such as first, and ways to put them together, such as sentence. Now we'll tell you about the selectors and
constructors for lists.
The function to select the first element of a list is called
car.[1] The function to select the
portion of a list containing all but the first element is called
cdr, which is pronounced "could-er." These are analogous to first and butfirst for words and sentences.
Of course, we can't extract pieces of a list that's empty, so we need a
predicate that will check for an empty list. It's called null? and it
returns #t for the empty list, #f for anything else. This is
the list equivalent of empty? for words and sentences.
There are two constructors for lists. The function list takes
any number of arguments and returns a list with those arguments as its
elements.
> (list (+ 2 3) 'squash (= 2 2) (list 4 5) remainder 'zucchini) (5 SQUASH #T (4 5) #<PROCEDURE> ZUCCHINI)
The other constructor, cons, is used when you already have
a list and you want to add one new element. Cons takes two arguments,
an element and a list (in that order), and returns a new list whose car is the first argument and whose cdr is the second.
> (cons 'for '(no one)) (FOR NO ONE) > (cons 'julia '()) (JULIA)
There is also a function that combines the elements of two or more lists into a larger list:
> (append '(get back) '(the word)) (GET BACK THE WORD)
It's important that you understand how list, cons,
and append differ from each other:
> (list '(i am) '(the walrus)) ((I AM) (THE WALRUS)) > (cons '(i am) '(the walrus)) ((I AM) THE WALRUS) > (append '(i am) '(the walrus)) (I AM THE WALRUS)
When list is invoked with two arguments, it considers them to be two
proposed elements for a new two-element list. List doesn't care
whether the arguments are themselves lists, words, or anything else; it just
creates a new list whose elements are the arguments. In this case, it ends
up with a list of two lists.
Cons requires that its second argument be a list.[2] Cons will extend that list to form a new list, one element
longer than the original; the first element of the resulting list comes from
the first argument to cons. In other words, when you pass cons
two arguments, you get back a list whose car is the first argument to
cons and whose cdr is the second argument.
Thus, in this example, the three elements of the returned list consist
of the first argument as one single element, followed by the elements
of the second argument (in this case, two words). (You may be wondering
why anyone would want to use such a strange constructor instead of list. The answer has to do with recursive procedures, but hang on for a few
paragraphs and we'll show you an example, which will help more than any
explanation we could give in English.)
Finally, append of two arguments uses the elements of both
arguments as elements of its return value.
Pictorially, list creates a list whose elements are the arguments:
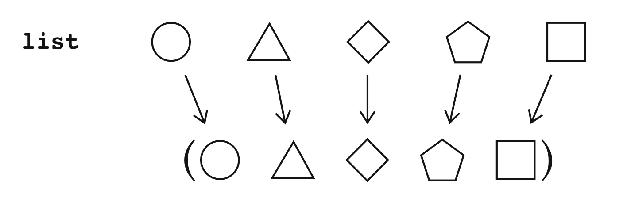
Cons creates an extension of its second argument with
one new element:
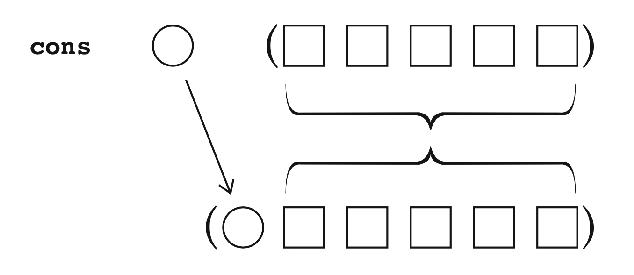
Append creates a list whose elements are the elements
of the arguments, which must be lists:
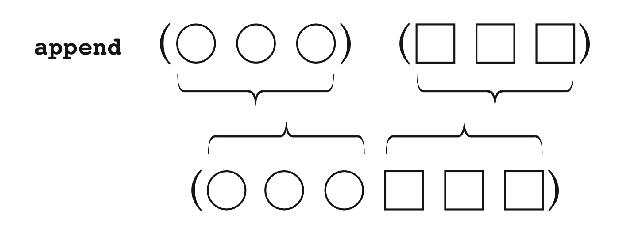
(define (praise flavors)
(if (null? flavors)
'()
(cons (se (car flavors) '(is delicious))
(praise (cdr flavors)))))
> (praise '(ginger (ultra chocolate) lychee (rum raisin)))
((GINGER IS DELICIOUS) (ULTRA CHOCOLATE IS DELICIOUS)
(LYCHEE IS DELICIOUS) (RUM RAISIN IS DELICIOUS))
In this example our result is a list of sentences. That is,
the result is a list that includes smaller lists as elements, but each of
these smaller lists is a sentence, in which only words are allowed. That's
why we used the constructor cons for the overall list, but se
for each sentence within the list.
This is the example worth a thousand words that we promised, to show why cons is useful. List wouldn't work in this situation. You can
use list only when you know exactly how many elements will be in your
complete list. Here, we are writing a procedure that works for any number of
elements, so we recursively build up the list, one element at a time.
In the following example we take advantage of structured lists to produce a translation dictionary. The entire dictionary is a list; each element of the dictionary, a single translation, is a two-element list; and in some cases a translation may involve a phrase rather than a single word, so we can get three deep in lists.
(define (translate wd) (lookup wd '((window fenetre) (book livre) (computer ordinateur) (house maison) (closed ferme) (pate pate) (liver foie) (faith foi) (weekend (fin de semaine)) ((practical joke) attrape) (pal copain)))) (define (lookup wd dictionary) (cond ((null? dictionary) '(parlez-vous anglais?)) ((equal? wd (car (car dictionary))) (car (cdr (car dictionary)))) (else (lookup wd (cdr dictionary))))) > (translate 'computer) ORDINATEUR > (translate '(practical joke)) ATTRAPE > (translate 'recursion) (PARLEZ-VOUS ANGLAIS?)
By the way, this example will help us explain why those ridiculous names
car and cdr haven't died out. In this not-so-hard program we
find ourselves saying
(car (cdr (car dictionary)))
to refer to the French part of the first translation in the
dictionary. Let's go through that slowly. (Car dictionary) gives us
the first element of the dictionary, one English-French pairing. Cdr
of that first element is a one-element list, that is, all but the English word
that's the first element of the pairing. What we want isn't the one-element
list but rather its only element, the French word, which is its car.
This car of cdr of car business is pretty lengthy and
awkward. But Scheme gives us a way to say it succinctly:
(cadar dictionary)
In general, we're allowed to use names like cddadr up to
four deep in As and Ds. That one means
(cdr (cdr (car (cdr something))))
or in other words, take the cdr of the cdr of the car of the cdr of its argument. Notice that the order of letters
A and D follows the order in which you'd write the procedure
names, but (as always) the procedure that's invoked first is the one on
the right. Don't make the mistake of reading cadr as meaning
"first take the car and then take the cdr." It means "take
the car of the cdr."
The most commonly used of these abbreviations are cadr, which selects
the second element of a list; caddr, which selects the third element;
and cadddr, which selects the fourth.
You've probably noticed that it's hard to distinguish between a sentence (which must be made up of words) and a list that happens to have words as its elements.
The fact is, sentences are lists. You could take car of a
sentence, for example, and it'd work fine. Sentences are an
abstract data type represented by lists. We created the sentence
ADT by writing special selectors and constructors that provide a
different way of using the same underlying machinery—a different
interface, a different metaphor, a different point of view.
How does our sentence point of view differ from the built-in Scheme point of view using lists? There are three differences:
| • | A sentence can contain only words, not sublists. |
|---|
| • | Sentence selectors are symmetrical front-to-back. |
|---|
| • | Sentences and words have the same selectors. |
|---|
All of these differences fit a common theme: Words and sentences are meant to represent English text. The three differences reflect three characteristics of English text: First, text is made of sequences of words, not complicated structures with sublists. Second, in manipulating text (for example, finding the plural of a noun) we need to look at the end of a word or sentence as often as at the beginning. Third, since words and sentences work together so closely, it makes sense to use the same tools with both. By contrast, from Scheme's ordinary point of view, an English sentence is just one particular case of a much more general data structure, whereas a symbol[3] is something entirely different.
The constructors and selectors for sentences reflect these three
differences. For example, it so happens that Scheme represents lists in a
way that makes it easy to find the first element, but harder to find the
last one. That's reflected in the fact that there are no primitive
selectors for lists equivalent to last and butlast for
sentences. But we want last and butlast to be a part of the
sentence package, so we have to write them in terms of the "real" Scheme
list selectors. (In the versions presented here, we are ignoring the issue
of applying the selectors to words.)
(define (first sent) ;;; just for sentences
(car sent))
(define (last sent)
(if (null? (cdr sent))
(car sent)
(last (cdr sent))))
(define (butfirst sent)
(cdr sent))
(define (butlast sent)
(if (null? (cdr sent))
'()
(cons (car sent) (butlast (cdr sent)))))
If you look "behind the curtain" at the implementation, last is a lot more complicated than first. But from the point of
view of a sentence user, they're equally simple.
In Chapter 16 we used the pattern matcher's known-values database to
introduce the idea of abstract data types. In that example, the most
important contribution of the ADT was to isolate the details of the
implementation, so that the higher-level procedures could invoke lookup and add without the clutter of looking for exclamation
points. We did hint, though, that the ADT represents a shift in how the
programmer thinks about the sentences that are used to represent databases;
we don't take the acronym of a database, even though the database is
a sentence and so it would be possible to apply the acronym procedure
to it. Now, in thinking about sentences, this idea of shift in viewpoint is
more central. Although sentences are represented as lists, they behave much
like words, which are represented quite differently.[4] Our sentence mechanism highlights the uses of
sentences, rather than the implementation.
The higher-order functions that we've used until now work only for
words and sentences. But the idea of higher-order functions applies
perfectly well to structured lists. The official list versions of every, keep, and accumulate are called map, filter,
and reduce.
Map takes two arguments, a function and a list, and returns a list
containing the result of applying the function to each element of the list.
> (map square '(9 8 7 6)) (81 64 49 36) > (map (lambda (x) (se x x)) '(rocky raccoon)) ((ROCKY ROCKY) (RACCOON RACCOON)) > (every (lambda (x) (se x x)) '(rocky raccoon)) (ROCKY ROCKY RACCOON RACCOON) > (map car '((john lennon) (paul mccartney) (george harrison) (ringo starr))) (JOHN PAUL GEORGE RINGO) > (map even? '(9 8 7 6)) (#F #T #F #T) > (map (lambda (x) (word x x)) 'rain) ERROR - INVALID ARGUMENT TO MAP: RAIN
The word "map" may seem strange for this function, but it comes
from the mathematical study of functions, in which they talk about a mapping of the domain into the range. In this terminology, one talks
about "mapping a function over a set" (a set of argument values, that is),
and Lispians have taken over the same vocabulary, except that we talk about
mapping over lists instead of mapping over sets. In any case, map is
a genuine Scheme primitive, so it's the official grownup way to talk about
an every-like higher-order function, and you'd better learn to like it.
Filter also takes a function and a list as arguments; it returns a
list containing only those elements of the argument list for which the
function returns a true value. This is the same as keep, except that
the elements of the argument list may be sublists, and their structure is
preserved in the result.
> (filter (lambda (flavor) (member? 'swirl flavor))
'((rum raisin) (root beer swirl) (rocky road) (fudge swirl)))
((ROOT BEER SWIRL) (FUDGE SWIRL))
> (filter word? '((ultra chocolate) ginger lychee (raspberry sherbet)))
(GINGER LYCHEE)
> (filter (lambda (nums) (= (car nums) (cadr nums)))
'((2 3) (4 4) (5 6) (7 8) (9 9)))
((4 4) (9 9))
Filter probably makes sense to you as a name; the metaphor
of the air filter that allows air through but doesn't allow dirt, and so on,
evokes something that passes some data and blocks other data. The only
problem with the name is that it doesn't tell you whether the elements for
which the predicate function returns #t are filtered in or filtered
out. But you're already used to keep, and filter works
the same way. Filter is not a standard Scheme primitive, but it's a
universal convention; everyone defines it the same way we do.
Reduce is just like accumulate except that it works only on
lists, not on words. Neither is a built-in Scheme primitive; both names are
seen in the literature. (The name "reduce" is official in the languages
APL and Common Lisp, which do include this higher-order function as a primitive.)
> (reduce * '(4 5 6))
120
> (reduce (lambda (list1 list2) (list (+ (car list1) (car list2))
(+ (cadr list1) (cadr list2))))
'((1 2) (30 40) (500 600)))
(531 642)
The list? predicate returns #t if its argument is a list, #f otherwise.
The predicate equal?, which we've discussed earlier as applied to
words and sentences, also works for structured lists.
The predicate member?, which we used in one of the
examples above, isn't a true Scheme primitive, but part of the word and
sentence package. (You can tell because it "takes apart" a word to look
at its letters separately, something that Scheme doesn't ordinarily do.)
Scheme does have a member primitive without the question mark that's
like member? except for two differences: Its second argument must be
a list (but can be a structured list); and instead of returning #t it
returns the portion of the argument list starting with the element equal to
the first argument. This will be clearer with an example:
> (member 'd '(a b c d e f g)) (D E F G) > (member 'h '(a b c d e f g)) #F
This is the main example in Scheme of the semipredicate
idea that we mentioned earlier in passing. It doesn't have a question mark
in its name because it returns values other than #t and #f,
but it works as a predicate because any non-#f value is considered
true.
The only word-and-sentence functions that we haven't already mentioned are
item and count. The list equivalent of item is called
list-ref
> (list-ref '(happiness is a warm gun) 3) WARM
The list equivalent of count is called length, and
it's exactly the same except that it doesn't work on words.
An example earlier in this chapter was about translating from English to
French. This involved searching for an entry in a list by comparing the
first element of each entry with the information we were looking for. A
list of names and corresponding values is called an association
list, or an a-list. The Scheme primitive assoc looks up a
name in an a-list:
> (assoc 'george
'((john lennon) (paul mccartney)
(george harrison) (ringo starr)))
(GEORGE HARRISON)
> (assoc 'x '((i 1) (v 5) (x 10) (l 50) (c 100) (d 500) (m 1000)))
(X 10)
> (assoc 'ringo '((mick jagger) (keith richards) (brian jones)
(charlie watts) (bill wyman)))
#F
(define dictionary
'((window fenetre) (book livre) (computer ordinateur)
(house maison) (closed ferme) (pate pate) (liver foie)
(faith foi) (weekend (fin de semaine))
((practical joke) attrape) (pal copain)))
(define (translate wd)
(let ((record (assoc wd dictionary)))
(if record
(cadr record)
'(parlez-vous anglais?))))
Assoc returns #f if it can't find the entry you're
looking for in your association list. Our translate procedure
checks for that possibility before using cadr to extract the French
translation, which is the second element of an entry.
In the beginning of this book we told you about some Scheme procedures that can take any number of arguments, but you haven't yet learned how to write such procedures for yourself, because Scheme's mechanism for writing these procedures requires the use of lists.
Here's a procedure that takes one or more numbers as arguments and returns true if these numbers are in increasing order:
(define (increasing? number . rest-of-numbers) (cond ((null? rest-of-numbers) #t) ((> (car rest-of-numbers) number) (apply increasing? rest-of-numbers)) (else #f))) > (increasing? 4 12 82) #T > (increasing? 12 4 82 107) #F
The first novelty to notice in this program is the dot in the first line.
In listing the formal parameters of a procedure, you can use a dot just
before the last parameter to mean that that parameter (rest-of-numbers
in this case) represents any number of arguments, including zero. The value
that will be associated with this parameter when the procedure is invoked
will be a list whose elements are the actual argument values.
In this example, you must invoke increasing? with at least one
argument; that argument will be associated with the parameter number.
If there are no more arguments, rest-of-numbers will be the empty
list. But if there are more arguments, rest-of-numbers will be a list
of their values. (In fact, these two cases are the same: Rest-of-numbers will be a list of all the remaining arguments, and if there
are no such arguments, rest-of-numbers is a list with no elements.)
The other novelty in this example is the procedure apply. It takes
two arguments, a procedure and a list. Apply invokes the given
procedure with the elements of the given list as its arguments, and returns
whatever value the procedure returns. Therefore, the following two
expressions are equivalent:
(+ 3 4 5) (apply + '(3 4 5))
We use apply in increasing? because we don't know how
many arguments we'll need in its recursive invocation. We can't just say
(increasing? rest-of-numbers)
because that would give increasing? a list as its single
argument, and it doesn't take lists as arguments—it takes numbers. We
want the numbers in the list to be the arguments.
We've used the name rest-of-numbers as the formal parameter to suggest
"the rest of the arguments," but that's not just an idea we made up. A
parameter that follows a dot and therefore represents a variable number of
arguments is called a rest parameter.
Here's a table showing the values of number and rest-of-numbers
in the recursive invocations of increasing? for the example
(increasing? 3 5 8 20 6 43 72) number rest-of-numbers 3 (5 8 20 6 43 72) 5 (8 20 6 43 72) 8 (20 6 43 72) 20 (6 43 72) (returns false at this point)
In the increasing? example we've used one formal parameter
before the dot, but you may use any number of such parameters, including zero.
The number of formal parameters before the dot determines the minimum number of arguments that must be used when your procedure is
invoked. There can be only one formal parameter after the dot.
Let's pretend we've stored this entire book in a gigantic Scheme list structure. It's a list of chapters. Each chapter is a list of sections. Each section is a list of paragraphs. Each paragraph is a list of sentences, which are themselves lists of words.
Now we want to know how many times the word "mathematicians" appears in the book. We could do it the incredibly boring way:
(define (appearances-in-book wd book)
(reduce + (map (lambda (chapter) (appearances-in-chapter wd chapter))
book)))
(define (appearances-in-chapter wd chapter)
(reduce + (map (lambda (section) (appearances-in-section wd section))
chapter)))
(define (appearances-in-section wd section)
(reduce + (map (lambda (paragraph)
(appearances-in-paragraph wd paragraph))
section)))
(define (appearances-in-paragraph wd paragraph)
(reduce + (map (lambda (sent) (appearances-in-sentence wd sent))
paragraph)))
(define (appearances-in-sentence given-word sent)
(length (filter (lambda (sent-word) (equal? sent-word given-word))
sent)))
but that would be incredibly boring.
What we're going to do is similar to the reasoning we used in developing the
idea of recursion in Chapter 11. There, we wrote a family of
procedures named downup1, downup2, and so on; we then noticed
that most of these procedures looked almost identical, and "collapsed"
them into a single recursive procedure. In the same spirit, notice that all
the appearances-in- procedures are very similar. We can make them
even more similar by rewriting the last one:
(define (appearances-in-sentence wd sent) (reduce + (map (lambda (wd2) (appearances-in-word wd wd2)) sent))) (define (appearances-in-word wd wd2) (if (equal? wd wd2) 1 0))
Now, just as before, we want to write a single procedure that combines all of these.
What's the base case? Books, chapters, sections, paragraphs, and sentences are all lists of smaller units. It's only when we get down to individual words that we have to do something different:
(define (deep-appearances wd structure)
(if (word? structure)
(if (equal? structure wd) 1 0)
(reduce +
(map (lambda (sublist) (deep-appearances wd sublist))
structure))))
> (deep-appearances
'the
'(((the man) in ((the) moon)) ate (the) potstickers))
3
> (deep-appearances 'n '(lambda (n) (if (= n 0) 1 (* n (f (- n 1))))))
4
> (deep-appearances 'mathematicians the-book-structure)
7
This is quite different from the recursive situations we've seen
before. What looks like a recursive call from deep-appearances to
itself is actually inside an anonymous procedure that will be called
repeatedly by map. Deep-appearances doesn't just call
itself once in the recursive case; it uses map to call itself for each
element of structure. Each of those calls returns a number; map
returns a list of those numbers. What we want is the sum of those numbers,
and that's what reduce will give us.
This explains why deep-appearances must accept words as well as lists
as the structure argument. Consider a case like
(deep-appearances 'foo '((a) b))
Since structure has two elements, map will call
deep-appearances twice. One of these calls uses the list (a) as
the second argument, but the other call uses the word b as the second
argument.
Of course, if structure is a word, we can't make recursive calls for
its elements; that's why words are the base case for this recursion. What
should deep-appearances return for a word? If it's the word we're
looking for, that counts as one appearance. If not, it counts as no
appearances.
You're accustomed to seeing the empty list as the base case in a recursive
list processing procedure. Also, you're accustomed to thinking of the base
case as the end of a complete problem; you've gone through all of
the elements of a list, and there are no more elements to find. In most
problems, there is only one recursive invocation that turns out to be a base
case. But in using deep-appearances, there are many
invocations for base cases—one for every word in the list structure.
Reaching a base case doesn't mean that we've reached the end of the entire
structure! You might want to trace a short example to help you understand
the sequence of events.
Although there's no official name for a structure made of lists of lists of
… of lists, there is a common convention for naming
procedures that deal with these structures; that's why we've called this
procedure deep-appearances. The word "deep" indicates that this
procedure is just like a procedure to look for the number of appearances of
a word in a list, except that it looks "all the way down" into the
sub-sub-⋅⋅⋅-sublists instead of just looking at the elements of the top-level
list.
This version of deep-appearances, in which higher-order procedures are
used to deal with the sublists of a list, is a common programming
style. But for some problems, there's another way to organize the same
basic program without higher-order procedures. This other organization
leads to very compact, but rather tricky, programs. It's also a widely used
style, so we want you to be able to recognize it.
Here's the idea. We deal with the base case—words—just as before. But
for lists we do what we often do in trying to simplify a list problem: We
divide the list into its first element (its car) and all the rest of
its elements (its cdr). But in this case, the resulting program is a
little tricky. Ordinarily, a recursive program for lists makes a recursive
call for the cdr, which is a list of the same kind as the whole
argument, but does something non-recursive for the car, which is just
one element of that list. This time, the car of the kind of structured
list-of-lists we're exploring may itself be a list-of-lists! So we make a
recursive call for it, as well:
(define (deep-appearances wd structure)
(cond ((equal? wd structure) 1) ; base case: desired word
((word? structure) 0) ; base case: other word
((null? structure) 0) ; base case: empty list
(else (+ (deep-appearances wd (car structure))
(deep-appearances wd (cdr structure))))))
This procedure has two different kinds of base case. The first
two cond clauses are similar to the base case in the previous version
of deep-appearances; they deal with a "structure" consisting of a
single word. If the structure is the word we're looking for, then the word
appears once in it. If the structure is some other word, then the word
appears zero times. The third clause is more like the base case of an
ordinary list recursion; it deals with an empty list, in which case the word
appears zero times in it. (This still may not be the end of the entire
structure used as the argument to the top-level invocation, but may instead
be merely the end of a sublist within that structure.)
If we reach the else clause, then the structure is neither a word
nor an empty list. It must, therefore, be a non-empty list, with a car
and a cdr. The number of appearances in the entire structure
of the word we're looking for is equal to the number of appearances in the
car plus the number in the cdr.
In deep-appearances the desired result is a single number. What if we
want to build a new list-of-lists structure? Having used car and cdr to disassemble a structure, we can use cons to build a new one.
For example, we'll translate our entire book into Pig Latin:
(define (deep-pigl structure) (cond ((word? structure) (pigl structure)) ((null? structure) '()) (else (cons (deep-pigl (car structure)) (deep-pigl (cdr structure)))))) > (deep-pigl '((this is (a structure of (words)) with) (a (peculiar) shape))) ((ISTHAY ISAY (AAY UCTURESTRAY OFAY (ORDSWAY)) ITHWAY) (AAY (ECULIARPAY) APESHAY))
Compare deep-pigl with an every-pattern list recursion
such as praise on page there. Both look like
(cons (something (car argument)) (something (cdr argument)))
And yet these procedures are profoundly different. Praise
is a simple left-to-right walk through the elements of a sequence;
deep-pigl dives in and out of sublists. The difference is a result
of the fact that praise does one recursive call, for the cdr,
while deep-pigl does two, for the car as well as the cdr.
The pattern exhibited by deep-pigl is called car-cdr
recursion. (Another name for it is "tree recursion," for a reason we'll
see in the next chapter.)
Just as we mentioned about the names word and sentence,
resist the temptation to use list as a formal parameter. We use
lst instead, but other alternatives are capital L or seq
(for "sequence").
The list constructor cons does not treat its two arguments
equivalently. The second one must be the list you're trying to extend.
There is no equally easy way to extend a list on the right (although you can
put the new element into a one-element list and use append). If you
get the arguments backward, you're likely to get funny-looking results that
aren't lists, such as
((3 . 2) . 1)
The result you get when you cons onto something that isn't a
list is called a pair. It's sometimes called a "dotted pair"
because of what it looks like when printed:
> (cons 'a 'b) (A . B)
It's just the printed representation that's dotted, however; the
dot isn't part of the pair any more than the parentheses around a list are
elements of the list. Lists are made of pairs; that's why cons can
construct lists. But we're not going to talk about any pairs that aren't part of lists, so you don't have to think about them at all,
except to know that if dots appear in your results you're consing
backward.
Don't get confused between lists and sentences. Sentences have no internal structure; the good aspect of this is that it's hard to make mistakes about building the structure, but the bad aspect is that you might need such a structure. You can have lists whose elements are sentences, but it's confusing if you think of the same structure sometimes as a list and sometimes as a sentence.
In reading someone else's program, it's easy not to notice that a
procedure is making two recursive calls instead of just one. If you notice
only the recursive call for the cdr, you might think you're looking at
a sequential recursion.
If you're writing a procedure whose argument is a list-of-lists, it may feel funny to let it also accept a word as the argument value. People therefore sometimes insist on a list as the argument, leading to an overly complicated base case. If your base case test says
(word? (car structure))
then think about whether you'd have a better-organized program if the base case were
(word? structure)
Remember that in a deep-structure recursion you may need two base
cases, one for reaching an element that isn't a sublist, and the other for
an empty list, with no elements at all. (Our deep-appearances
procedure is an example.) Don't forget the empty-list case.
17.1 What will Scheme print in response to each of the following expressions? Try to figure it out in your head before you try it on the computer.
> (car '(Rod Chris Colin Hugh Paul))
> (cadr '(Rod Chris Colin Hugh Paul))
> (cdr '(Rod Chris Colin Hugh Paul))
> (car 'Rod)
> (cons '(Rod Argent) '(Chris White))
> (append '(Rod Argent) '(Chris White))
> (list '(Rod Argent) '(Chris White))
> (caadr '((Rod Argent) (Chris White)
(Colin Blunstone) (Hugh Grundy) (Paul Atkinson)))
> (assoc 'Colin '((Rod Argent) (Chris White)
(Colin Blunstone) (Hugh Grundy) (Paul Atkinson)))
> (assoc 'Argent '((Rod Argent) (Chris White)
(Colin Blunstone) (Hugh Grundy) (Paul Atkinson)))
17.2 For each of the following examples, write a procedure of two arguments that, when applied to the sample arguments, returns the sample result. Your procedures may not include any quoted data.
> (f1 '(a b c) '(d e f)) ((B C D)) > (f2 '(a b c) '(d e f)) ((B C) E) > (f3 '(a b c) '(d e f)) (A B C A B C) > (f4 '(a b c) '(d e f)) ((A D) (B C E F))
17.3 Describe the value returned by this invocation of map:
> (map (lambda (x) (lambda (y) (+ x y))) '(1 2 3 4))
17.4 Describe the result of calling the following procedure with a list as its argument. (See if you can figure it out before you try it.)
(define (mystery lst)
(mystery-helper lst '()))
(define (mystery-helper lst other)
(if (null? lst)
other
(mystery-helper (cdr lst) (cons (car lst) other))))
17.5 Here's a procedure that takes two numbers as arguments and returns whichever number is larger:
(define (max2 a b) (if (> b a) b a))
Use max2 to implement max, a procedure that takes
one or more numeric arguments and returns the largest of them.
17.6 Implement append using car, cdr, and cons.
(Note: The built-in append can take any number of arguments.
First write a version that accepts only two arguments. Then,
optionally, try to write a version that takes any number.)
17.7 Append may remind you of sentence. They're similar, except that
append works only with lists as arguments, whereas sentence will
accept words as well as lists. Implement sentence using append. (Note: The built-in sentence can take any number of
arguments. First write a version that accepts only two
arguments. Then, optionally, try to write a version that takes any
number. Also, you don't have to worry about the error checking that the
real sentence does.)
17.8 Write member.
17.9 Write list-ref.
17.10 Write length.
17.11 Write before-in-list?, which takes a list and two elements of
the list. It should return #t if the second argument appears in the
list argument before the third argument:
> (before-in-list? '(back in the ussr) 'in 'ussr) #T > (before-in-list? '(back in the ussr) 'the 'back) #F
The procedure should also return #f if either of the supposed elements
doesn't appear at all.
17.12 Write a procedure called flatten that takes as its argument a
list, possibly including sublists, but whose ultimate building blocks are
words (not Booleans or procedures). It should return a sentence containing
all the words of the list, in the order in which they appear in the original:
> (flatten '(((a b) c (d e)) (f g) ((((h))) (i j) k))) (A B C D E F G H I J K)
17.13 Here is a procedure that counts the number of words anywhere within a structured list:
(define (deep-count lst) (cond ((null? lst) 0) ((word? (car lst)) (+ 1 (deep-count (cdr lst)))) (else (+ (deep-count (car lst)) (deep-count (cdr lst))))))
Although this procedure works, it's more complicated than necessary. Simplify it.
17.14 Write a procedure branch that takes as arguments a list of
numbers and a nested list structure. It should be the list-of-lists equivalent
of item, like this:
> (branch '(3) '((a b) (c d) (e f) (g h))) (E F) > (branch '(3 2) '((a b) (c d) (e f) (g h))) F > (branch '(2 3 1 2) '((a b) ((c d) (e f) ((g h) (i j)) k) (l m))) H
In the last example above, the second element of the list is
((C D) (E F) ((G H) (I J)) K)
The third element of that smaller
list is ((G H) (I J)); the first element of that is (G H); and
the second element of that is just H.
17.15 Modify the pattern matcher to represent the known-values database as a
list of two-element lists, as we suggested at the beginning of this chapter.
17.16 Write a predicate valid-infix? that takes a list as argument
and returns #t if and only if the list is a legitimate infix
arithmetic expression (alternating operands and operators, with
parentheses—that is, sublists—allowed for grouping).
> (valid-infix? '(4 + 3 * (5 - 2))) #T > (valid-infix? '(4 + 3 * (5 2))) #F
Cdr, coming up in the next
sentence, stands for "contents of decrement register." The names seem
silly in the Lisp context, but that's because the Lisp people used these
register components in ways the computer designers didn't intend. Anyway,
this is all very interesting to history buffs but irrelevant to our
purposes. We're just showing off that one of us is actually old enough to
remember these antique computers first-hand.[2] This is not the whole story. See the "pitfalls" section for a slightly expanded version.
[3] As we said in Chapter 5, "symbol" is the official name for words that are neither strings nor numbers.
[4] We implemented words by combining three data types that are primitive in Scheme: strings, symbols, and numbers.
Brian Harvey,
bh@cs.berkeley.edu