


|
|
This is a big program and you can't keep it all in your head at once. In this chapter, we'll discuss different parts of the program separately. For example, while we're talking about the screen display procedures, we'll just take the rest of the program for granted. We'll assume that we can ask for the value in a cell, and some other part of the program will ensure that we can find it out.
Our division of the program includes these parts:
| • | The command processor, which reads user commands and oversees their execution. |
|---|
| • | The specific commands: cell selection commands, load, and put.
|
|---|
| • | The formula translator, which turns a formula into an expression by translating relative cell positions to specific cells. |
|---|
| • | The dependency manager, which keeps track of which cells' expressions depend on which other cells. |
|---|
| • | The expression evaluator. |
|---|
| • | The screen printer. |
|---|
| • | The cell management procedures, which store and retrieve cell information for the rest of the program. |
|---|
The diagram below shows the interconnections among these seven parts of the program by showing what information they have to provide for each other.
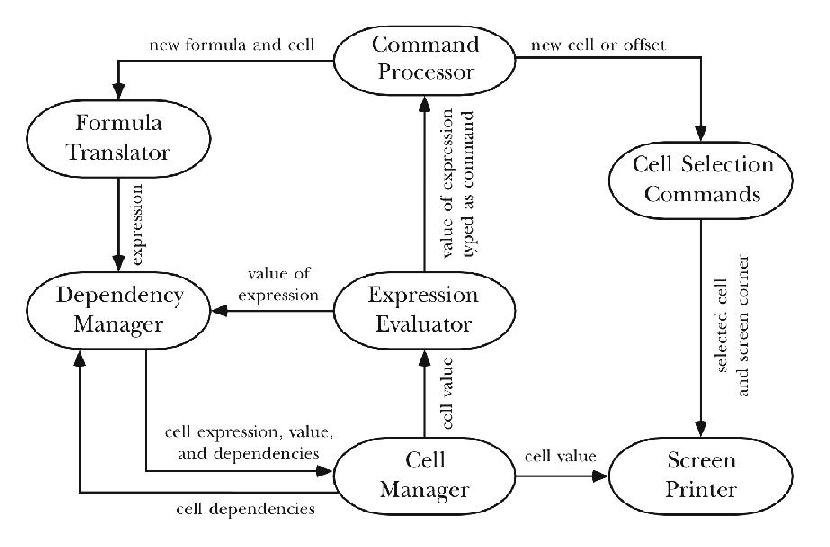
(The arrows that aren't in the diagram convey as much information as the ones that are. For example, since there is no arrow from the evaluator to the printer, we know that when the spreadsheet program redisplays the screen, the values printed are found directly in the data structure; no new computation of formulas is needed.)
The spreadsheet program does its work by manipulating cells. In this section we introduce three abstract data types having to do with cells. Before we jump into the spreadsheet procedures themselves, we must introduce these three types, which are used throughout the program.
Each cell is a data structure that contains various pieces of information, including its value and other things that we'll talk about later. Just as these cells are arranged in a two-dimensional pattern on the screen, they are kept within the program in a two-dimensional data structure: a vector of vectors.
The elements of a vector are selected by number, using vector-ref.
Therefore, if we're looking for a particular cell, such as c5, what
the program really wants to know is that this cell is in column 3, row
5.[1] If the program refers to cells by
name, then there will be several occasions for it to split the word c5
into its pieces c and 5, and to convert the letter c into
the number 3. These operations are fairly slow. To avoid carrying them out
repeatedly, the spreadsheet program identifies cells internally using a form
that's invisible to the person using the program, called a "cell ID."
Therefore, there are three different abstract data types in the
program that have to do with cells: cell names, such as c5; cell IDs;
and cells themselves. We've chosen to represent cell IDs as three-element
lists like this one:
(id 3 5)
but you won't see much evidence of that fact within the program
because we've implemented selectors and constructors for all of these three
types. The representation includes the word id because one facility
that the program needs is the ability to determine whether some datum is or
is not a cell ID. The predicate cell-id? looks for a list whose first
element is id.
The selectors for cell IDs are id-row and id-col; both take a
cell ID as argument and return a number. The constructor, make-id,
takes a column number (not a letter) and a row number as arguments.
When the program recognizes a cell name typed by the user, it calls cell-name->id to translate the name to an ID, and only the ID is stored for
later use.
(These application-specific ADTs are similar to the database of known values in the pattern matcher, as opposed to more general-purpose ADTs like trees and sentences.)
Here's the core of the command processor:
(define (command-loop)
(print-screen)
(let ((command-or-formula (read)))
(if (equal? command-or-formula 'exit)
"Bye!"
(begin (process-command command-or-formula)
(command-loop)))))
This short program runs until the user types exit, because
it invokes itself as its last step. During each invocation, it prints the
current spreadsheet display, uses read to read a command, and
carries out whatever actions that command requires. Those actions probably
change something in the spreadsheet data, so the next cycle has to redisplay
the modified data before accepting another command.
Print-screen is a large chunk of the program and will be discussed
in its own section.
How does process-command work? It looks for the command name (a word
such as put) in its list of known commands. The commands are kept in an
association list, like this:
((p …) (n …) (b …) (f …) (select …) (put …) (load …))
Each of these sublists contains two elements: the name and the procedure that carries out the command. We'll see shortly how these procedures are invoked.
Looking for the command name is a little tricky because in the spreadsheet
language a command can be invoked either by typing its name inside
parentheses with arguments, as in Scheme, or by typing the name alone,
without parentheses, which Scheme wouldn't interpret as a request to invoke
a procedure. For example, the argument to process-command might be a
list, such as (f 3), or just a word, such as f. A third case is
that the argument might not be one of these commands at all, but instead
might be a formula, just like one that could be used to determine the value
in a cell. Process-command must recognize these three cases:
(define (process-command command-or-formula) (cond ((and (list? command-or-formula) (command? (car command-or-formula))) (execute-command command-or-formula)) ((command? command-or-formula) (execute-command (list command-or-formula 1))) (else (exhibit (ss-eval (pin-down command-or-formula (selection-cell-id)))))))
The command? predicate tells whether its argument is one of
the command names in the list. As you can see, if a command name is used
without parentheses, process-command pretends that it was given an
argument of 1.
Execute-command looks up the command name in the list of commands,
then applies the associated procedure to the arguments, if any:
(define (execute-command command) (apply (get-command (car command)) (cdr command)))
The else clause in process-command, which handles the case
of a formula typed instead of a command, invokes several procedures
that you haven't seen yet. We'll explain them when we get to the section of
the program that manipulates formulas. The only one that's used just for
command processing is exhibit:
(define (exhibit val) (show val) (show "Type RETURN to redraw screen") (read-line) (read-line))
This prints a value on the screen, gives the user a chance to read
it, and then, when the user is ready, returns to processing commands. (This
will entail redrawing the spreadsheet display; that's why we have to wait for
the user to hit return.) The reason that we invoke read-line twice is
that the call to read from command-loop reads the spreadsheet
formula you typed but doesn't advance to the next line. Therefore, the
first read-line invocation gobbles that empty line; the second call to
read-line reads the (probably empty) line that the user typed in
response to the prompting message.[2]
Several commands have to do with selecting a cell. We'll show just one
typical procedure, the one that carries out the p (previous row)
command:
(define (prev-row delta)
(let ((row (id-row (selection-cell-id))))
(if (< (- row delta) 1)
(error "Already at top.")
(set-selected-row! (- row delta)))))
(define (set-selected-row! new-row)
(select-id! (make-id (id-column (selection-cell-id)) new-row)))
(define (select-id! id)
(set-selection-cell-id! id)
(adjust-screen-boundaries))
Prev-row must ensure that the selected cell is within the
legal boundaries. Since prev-row only moves upward, it has to check
only that we don't go beyond row 1. (Next-row will instead check that
we don't go beyond row 30 in the other direction.)
Adjust-screen-boundaries checks for the situation in which the newly
selected cell, although within the bounds of the spreadsheet, is not within
the portion currently visible on the screen. In that case the visible
portion is shifted to include the selected cell. (The procedure is
straightforward and uninteresting, so we're not showing it here. You can
see it in the complete listing of the spreadsheet program at the end of this
chapter.)
Selection-cell-id is a procedure that returns the cell ID of the
cell that's currently selected. Similarly, set-selection-cell-id! sets the
current selection. There are comparable procedures screen-corner-cell-id and set-screen-corner-cell-id! to keep track of
which cell should be in the upper left corner of the screen display. There
is a vector named *special-cells* that holds these two cell IDs; you
can see the details in the complete program listing.
Load CommandLoading commands from files is easy. The command-loop procedure,
which carries out commands from the keyboard, repeatedly reads a command
with read and invokes process-command to carry it out. To load
commands from a file, we want to do exactly the same thing, except that we
read from a file instead of from the keyboard:
(define (spreadsheet-load filename)
(let ((port (open-input-file filename)))
(sl-helper port)
(close-input-port port)))
(define (sl-helper port)
(let ((command (read port)))
(if (eof-object? command)
'done
(begin (show command)
(process-command command)
(sl-helper port)))))
Put CommandThe put command takes two arguments, a formula and a place to put it.
The second of these can specify either a single cell or an entire row or
column. (If there is no second argument, then a single cell, namely the
selected cell, is implied.) Put invokes put-formula-in-cell
either once or several times, as needed. If only a single cell is involved,
then put calls put-formula-in-cell directly. If a row or column
is specified, then put uses the auxiliary procedure put-all-cells-in-row or put-all-cells-in-col as an intermediary.
(define (put formula . where) (cond ((null? where) (put-formula-in-cell formula (selection-cell-id))) ((cell-name? (car where)) (put-formula-in-cell formula (cell-name->id (car where)))) ((number? (car where)) (put-all-cells-in-row formula (car where))) ((letter? (car where)) (put-all-cells-in-col formula (letter->number (car where)))) (else (error "Put it where?"))))
The only tricky part of this is the first line. Put can be
invoked with either one or two arguments. Therefore, the dot notation is
used to allow a variable number of arguments; the parameter where will
have as its value not the second argument itself, but a list that either
contains the second argument or is empty. Thus, if there is a second
argument, put refers to it as (car where).
(define (put-all-cells-in-row formula row)
(put-all-helper formula (lambda (col) (make-id col row)) 1 26))
(define (put-all-cells-in-col formula col)
(put-all-helper formula (lambda (row) (make-id col row)) 1 30))
(define (put-all-helper formula id-maker this max)
(if (> this max)
'done
(begin (try-putting formula (id-maker this))
(put-all-helper formula id-maker (+ 1 this) max))))
(define (try-putting formula id)
(if (or (null? (cell-value id)) (null? formula))
(put-formula-in-cell formula id)
'do-nothing))
Put-all-cells-in-row and put-all-cells-in-col invoke
put-all-helper, which repeatedly puts the formula into a
cell.[3] Put-all-helper is a typical sequential recursion: Do
something for this element, and recur for the remaining elements. The
difference is that "this element" means a cell ID that combines one
constant index with one index that varies with each recursive call. How are
those two indices combined? What differs between filling a row and filling
a column is the function used to compute each cell ID.
The substitution model explains how the lambda expressions used as
arguments to put-all-helper implement this idea. Suppose we are
putting a formula into every cell in row 4. Then put-all-cells-in-row
will be invoked with the value 4 substituted for the parameter row. After this substitution, the body is
(put-all-helper formula (lambda (col) (make-id col 4)) 1 26)
The lambda expression creates a procedure that takes a
column number as argument and returns a cell ID for the cell in row 4 and
that column. This is just what put-all-helper needs. It invokes the
procedure with the varying column number as its argument to get the proper
cell ID.
Put-all-helper doesn't directly invoke put-formula-in-cell. The
reason is that if a particular cell already has a value, then the new
formula isn't used for that particular cell, unless the formula is empty.
That is, you can erase an entire row or column at once, but a non-empty
formula affects only cells that were empty before this command. Try-putting decides whether or not to put the formula into each possible
cell. (In try-putting, the third argument to if could be
anything; we're interested only in what happens if the condition is true.)
All that's left is, finally, to put the formula into a cell:
(define (put-formula-in-cell formula id) (put-expr (pin-down formula id) id))
The two new procedures seen here, pin-down and put-expr, are both large sections of the program and are described in the
next two sections of this chapter.
Suppose the user has said
(put (* (cell b) (cell c)) d)
The put procedure puts this formula into each cell of column
d by repeatedly calling put-formula-in-cell; as an example,
let's concentrate on cell d4.
The purpose of the formula is that later we're going to use it to compute a
value for d4. For that purpose, we will need to multiply two
particular numbers together: the ones in cells b4 and c4.
Although the same formula applies to cell d5, the particular numbers
multiplied together will be found in different places. So instead of
storing the same general formula in every d cell, what we'd really
like to store in d4 is something that refers specifically to b4 and c4.
We'll use the term "expression" for a formula whose cell references have
been replaced by specific cell IDs. We started with the idea that we wanted
to put a formula into a cell; we've refined that idea so that we now want to
put an expression into the cell. This goal has two parts: We must
translate the formula (as given to us by the user in the put command)
to an expression, and we must store that expression in the cell data
structure. These two subtasks are handled by pin-down, discussed in
this section, and by put-expr, discussed in the next section. Pin-down is entirely functional; the only modification to the spreadsheet
program's state in this process is carried out by put-expr.
We'll refer to the process of translating a formula to an expression as
"pinning down" the formula; the procedure pin-down carries out this
process. It's called "pinning down" because we start with a general formula and end up with a specific expression. Pin-down takes two arguments: The first is, of course, a formula; the
second is the ID of the cell that will be used as the reference point for
relative cell positions. In the context of the put command, the
reference point is the cell into which we'll put the expression. But pin-down doesn't think about putting anything anywhere; its job is to
translate a formula (containing relative cell locations) into an expression
(containing only absolute cell IDs).[4] Pin-down needs a reference point
as a way to understand the notation <3, which means "three
cells before the reference point."
Let's go back to the specific example. Put-formula-in-cell will invoke
(pin-down '(* (cell b) (cell c)) 'd4)
and pin-down will return the expression
(* (id 2 4) (id 3 4))
The overall structure of this problem is tree recursive. That's because a formula can be arbitrarily complicated, with sublists of sublists, just like a Scheme expression:
(put (+ (* (cell b) (cell c)) (- (cell 2< 3>) 6)) f)
Here's pin-down:
(define (pin-down formula id) (cond ((cell-name? formula) (cell-name->id formula)) ((word? formula) formula) ((null? formula) '()) ((equal? (car formula) 'cell) (pin-down-cell (cdr formula) id)) (else (bound-check (map (lambda (subformula) (pin-down subformula id)) formula)))))
The base cases of the tree recursion are specific cell names, such
as c3; other words, such as numbers and procedure names, which are
unaffected by pin-down; null formulas, which indicate that the user is
erasing the contents of a cell; and sublists that start with the word cell. The first three of these are trivial; the fourth, which we will
describe shortly, is the important case. If a formula is not one of these
four base cases, then it's a compound expression. In that case, we have to
pin down all of the subexpressions individually. (We basically map
pin-down over the formula. That's what makes this process tree
recursive.)
One complication is that the pinned-down formula might refer to nonexistent cells. For example, saying
(put (+ (cell 2< 3<) 1) d)
refers to cells in column b (two to the left of d)
three rows above the current row. That works for a cell such as d7,
referring to cell b4, but not for d2, which has no row that's
three above it. (There is no row -1.) So our program must refrain
from pinning down this formula for cells d1, d2, and d3.
Pin-down will instead return the word out-of-bounds to signal
this situation.
The case of a nonexistent cell is discovered by pin-down-cell at the
base of a tree recursion. The out-of-bounds signal must be returned
not only by the base case but by the initial invocation of pin-down.
That's why bound-check is used to ensure that if any part of a formula
is out of bounds, the entire formula will also be considered out of bounds:
(define (bound-check form)
(if (member 'out-of-bounds form)
'out-of-bounds
form))
When a formula contains a (cell …) sublist, the procedure pin-down-cell is invoked to translate that notation into a cell ID.
The arguments to pin-down-cell are a list of the "arguments" of the
cell sublist and the reference point's cell ID. (The word
"arguments" is in quotation marks because the word cell doesn't
represent a Scheme procedure, even though the parenthesized notation looks
like an invocation. In a way, the special treatment of cell by pin-down is analogous to the treatment of special forms, such as cond,
by the Scheme evaluator.)
There can be one or two of these "arguments" to cell. A single
argument is either a number, indicating a row, or a letter, indicating a
column. Two arguments specify both a column and a row, in that order:
(define (pin-down-cell args reference-id) (cond ((null? args) (error "Bad cell specification: (cell)")) ((null? (cdr args)) (cond ((number? (car args)) ; they chose a row (make-id (id-column reference-id) (car args))) ((letter? (car args)) ; they chose a column (make-id (letter->number (car args)) (id-row reference-id))) (else (error "Bad cell specification:" (cons 'cell args))))) (else (let ((col (pin-down-col (car args) (id-column reference-id))) (row (pin-down-row (cadr args) (id-row reference-id)))) (if (and (>= col 1) (<= col 26) (>= row 1) (<= row 30)) (make-id col row) 'out-of-bounds)))))
In the two-argument case, the job of pin-down-col and pin-down-row is to understand notations like <3 for relative
rows and columns:
(define (pin-down-col new old) (cond ((equal? new '*) old) ((equal? (first new) '>) (+ old (bf new))) ((equal? (first new) '<) (- old (bf new))) ((letter? new) (letter->number new)) (else (error "What column?")))) (define (pin-down-row new old) (cond ((number? new) new) ((equal? new '*) old) ((equal? (first new) '>) (+ old (bf new))) ((equal? (first new) '<) (- old (bf new))) (else (error "What row?"))))
The remaining part of the put command is put-expr, which actually
stores the translated expression in the cell data structure. You might
imagine that putting an expression into a cell would require nothing more
than invoking a mutator, like this:
(define (put-expr expr cell) ;; wrong (set-cell-expr! cell expr))
The trouble is that adding an expression to a cell might have many consequences beyond the mutation itself. For example, suppose we say
(put (+ a3 b2) c4)
If cells a3 and b2 already have values, we can't just
put the formula into c4; we must also compute its value and put that
value into c4.
Also, once c4 has a value, that could trigger the computation of
some other cell's value. If we've previously said
(put (+ a3 c4) b5)
then we're now able to compute a value for b5 because both
of the cells that it depends on have values.
All this implies that what's inside a cell is more than just an expression, or even an expression and a value. Each cell needs to know which other cells it depends on for its value, and also which other cells depend on it.
Our program represents each cell as a four-element vector. Each cell
includes a value, an expression, a list of parents (the cells that it
depends on), and a list of children (the cells that depend on it).
The latter two lists contain cell IDs. So our example cell c4 might
look like this:
#(12 (+ (id 1 3) (id 2 2)) ((id 1 3) (id 2 2)) ((id 2 5)))
In a simpler case, suppose we put a value into a cell that nothing depends on, by saying, for example,
(put 6 a1)
Then cell a1 would contain
#(6 6 () ())
(Remember that a value is just a very simple formula.)
There are selectors cell-value and so on that take a cell ID as
argument, and mutators set-cell-value! and so on that take a cell ID
and a new value as arguments. There's also the constructor make-cell,
but it's called only at the beginning of the program, when the 780 cells in
the spreadsheet are created at once.
When a cell is given a new expression, several things change:
| • | The new expression becomes the cell's expression, of course. |
|---|
| • | The cells mentioned in the expression become the parents of this cell. |
|---|
| • | This cell becomes a child of the cells mentioned in the expression. |
|---|
| • | If all the parents have values, the value of this cell is computed. |
|---|
Some of these changes are simple, but others are complicated. For example, it's not enough to tell the cell's new parents that the cell is now their child (the third task). First we have to tell the cell's old parents that this cell isn't their child any more. That has to be done before we forget the cell's old parents.
Here is an example. (In the following tables, we represent the data structures as if cells were represented by their names, even though really their IDs are used. We've done this to make the example more readable.) Suppose that we have five cells set up like this:
| cell | expression | value | parents | children |
|---|---|---|---|---|
a1 | 20
| 20 | () | (a2)
|
b1 | 5 | 5 | ()
| (a2 b2)
|
c1 | 8 | 8 | ()
| ()
|
a2 | (+ a1 b1) | 25
| (a1 b1) | (b2)
|
b2 | (+ a2 b1) | 30
| (a2 b1) | ()
|
If we now enter the spreadsheet command
(put (+ b1 c1) a2)
the program must first remove a2 from the children of its
old parents (changes are shown in boldface):
| cell | expression | value | parents | children |
|---|---|---|---|---|
a1 | 20
| 20 | () | ()
|
b1 | 5 | 5 | ()
| (b2)
|
c1 | 8 | 8 | ()
| ()
|
a2 | (+ a1 b1) | 25
| (a1 b1) | (b2)
|
b2 | (+ a2 b1) | 30
| (a2 b1) | ()
|
Then the program can change the expression and compute a new list of parents:
| cell | expression | value | parents | children |
|---|---|---|---|---|
a1 | 20
| 20 | () | ()
|
b1 | 5 | 5 | ()
| (b2)
|
c1 | 8 | 8 | ()
| ()
|
a2 | (+ b1 c1)
| 25 | (b1 c1)
| (b2)
|
b2 | (+ a2 b1) | 30
| (a2 b1) | ()
|
Next it can tell the new parents to add a2 as a
child, and can compute a2's new value:
| cell | expression | value | parents | children |
|---|---|---|---|---|
a1 | 20
| 20 | () | ()
|
b1 | 5 | 5 | ()
| (a2 b2)
|
c1 | 8 | 8 | ()
| (a2)
|
a2 | (+ b1 c1)
| 13 | (b1 c1)
| (b2)
|
b2 | (+ a2 b1) | 30
| (a2 b1) | ()
|
Changing a2's value affects the values of all of its
children, and also its grandchildren and so on (except that in this example
there are no grandchildren):
| cell | expression | value | parents | children |
|---|---|---|---|---|
a1 | 20
| 20 | () | ()
|
b1 | 5 | 5 | ()
| (a2 b2)
|
c1 | 8 | 8 | ()
| (a2)
|
a2 | (+ b1 c1)
| 13 | (b1 c1)
| (b2)
|
b2 | (+ a2 b1)
| 18 | (a2 b1) | ()
|
Now that we've considered an example, here is the main procedure that oversees all these tasks:
(define (put-expr expr-or-out-of-bounds id)
(let ((expr (if (equal? expr-or-out-of-bounds 'out-of-bounds)
'()
expr-or-out-of-bounds)))
(for-each (lambda (old-parent)
(set-cell-children!
old-parent
(remove id (cell-children old-parent))))
(cell-parents id))
(set-cell-expr! id expr)
(set-cell-parents! id (remdup (extract-ids expr)))
(for-each (lambda (new-parent)
(set-cell-children!
new-parent
(cons id (cell-children new-parent))))
(cell-parents id))
(figure id)))
Remember that put-expr's first argument is the return value
from pin-down, so it might be the word out-of-bounds instead of
an expression. In this case, we store an empty list as the expression,
indicating that there is no active expression for this cell.
Within the body of the let there are five Scheme expressions, each of
which carries out one of the tasks we've listed. The first expression tells
the cell's former parents that the cell is no longer their child. The second
expression stores the expression in the cell.
The third Scheme expression invokes extract-ids to find all the cell
ids used in expr, removes any duplicates, and establishes those
identified cells as the argument cell's parents. (You wrote remdup in
Exercise 14.3.) For example, if the expr is
(+ (id 4 2) (* (id 1 3) (id 1 3)))
then extract-ids will return the list
((id 4 2) (id 1 3) (id 1 3))
and remdup of that will be
((id 4 2) (id 1 3))
The fourth expression in the let tells each of the new parents to
consider the argument cell as its child. The fifth expression may or may
not compute a new value for this cell. (As we'll see in a moment, that
process is a little complicated.)
Two of these steps require closer examination. Here is the procedure used in the third step:
(define (extract-ids expr) (cond ((id? expr) (list expr)) ((word? expr) '()) ((null? expr) '()) (else (append (extract-ids (car expr)) (extract-ids (cdr expr))))))
This is a tree recursion. The first three cond clauses are
base cases; cell IDs are included in the returned list, while other words
are ignored. For compound expressions, we use the trick of making recursive
calls on the car and cdr of the list. We combine the results
with append because extract-ids must return a flat list of
cell IDs, not a cheap tree.
The fifth step in put-expr is complicated because, as we saw in the
example, changing the value of one cell may require us to recompute the
value of other cells:
(define (figure id)
(cond ((null? (cell-expr id)) (setvalue id '()))
((all-evaluated? (cell-parents id))
(setvalue id (ss-eval (cell-expr id))))
(else (setvalue id '()))))
(define (all-evaluated? ids)
(cond ((null? ids) #t)
((not (number? (cell-value (car ids)))) #f)
(else (all-evaluated? (cdr ids)))))
(define (setvalue id value)
(let ((old (cell-value id)))
(set-cell-value! id value)
(if (not (equal? old value))
(for-each figure (cell-children id))
'do-nothing)))
Figure is invoked for the cell whose expression we've just
changed. If there is no expression (that is, if we've changed it to an empty
expression or to an out-of-bounds one), then figure will remove any old
value that might be left over from a previous expression. If there is an
expression, then figure will compute and save a new value, but only if
all of this cell's parents have numeric values. If any parent doesn't have
a value, or if its value is a non-numeric label, then figure has to
remove the value from this cell.
Setvalue actually puts the new value in the cell. It first looks up
the old value. If the new and old values are different, then all of the
children of this cell must be re-figured. This, too, is a tree
recursion because there might be several children, and each of them might
have several children.
We haven't yet explained how ss-eval actually computes the value from
the expression. That's the subject of the next major part of the program.
Figure invokes ss-eval to convert a cell's expression into its
value. Also, we've seen earlier that process-command uses ss-eval to evaluate an expression that the user types in response to a
spreadsheet prompt. (That is, ss-eval is invoked if what the user
types isn't one of the special commands recognized by process-command
itself.)
The ss in ss-eval stands for "spreadsheet"; it distinguishes
this procedure from eval, a primitive procedure that evaluates
Scheme expressions. As it turns out, ss-eval's algorithm is
similar in many ways to that of Scheme's eval, although ss-eval
is much simpler in other ways. The experience you already have with
Scheme's expression evaluation will help you understand the spreadsheet's.
Scheme's evaluator takes an expression and computes the corresponding value. The expressions look quite different from the values, but there are well-defined rules (the ones we studied in Chapter 3) to translate expressions to values. In the spreadsheet language, as in Scheme, an expression can be one of three things:
| • | a constant expression (a number or quoted word), whose value is itself. |
|---|
| • | a variable (a cell ID, in the case of the spreadsheet language). |
|---|
| • | a procedure invocation enclosed in parentheses. |
|---|
The spreadsheet language is simpler than Scheme for three main reasons.
| • | There are no special forms such as if or define.[5]
|
|---|
| • | The only variables, the cell IDs, are global; in Scheme, much of the complexity of evaluation has to do with variables that are local to procedures (i.e., formal parameters). |
|---|
| • | The only procedures are primitives, so there is no need to evaluate procedure bodies. |
|---|
The structure of ss-eval is a cond whose clauses handle the
three types of expressions. Constants and variables are easy;
invocations require recursively evaluating the arguments before the
procedure can be invoked.
(define (ss-eval expr) (cond ((number? expr) expr) ((quoted? expr) (quoted-value expr)) ((id? expr) (cell-value expr)) ((invocation? expr) (apply (get-function (car expr)) (map ss-eval (cdr expr)))) (else (error "Invalid expression:" expr))))
The value of a number is itself; the value of a quoted word is the word
without the quotation mark. (Actually, by the time ss-eval sees a
quoted word, Scheme has translated the 'abc notation into (quote abc) and that's what we deal with here. Also, double-quoted strings
look different to the program from single-quoted words.)
(define (quoted? expr)
(or (string? expr)
(and (list? expr) (equal? (car expr) 'quote))))
(define (quoted-value expr)
(if (string? expr)
expr
(cadr expr)))
The third clause checks for a cell ID; the value of such an expression is the value stored in the corresponding cell.
If an expression is none of those things, it had better be a function
invocation, that is, a list. In that case, ss-eval has to do three
things: It looks up the function name in a table (as we did earlier for
spreadsheet commands); it recursively evaluates all the argument
subexpressions; and then it can invoke apply to apply the procedure to
the argument values.
Get-function looks up a function name in the name-to-function
association list and returns the corresponding Scheme procedure. Thus, only
the functions included in the list can be used in spreadsheet formulas.
The entire expression evaluator, including ss-eval and its helper
procedures, is functional. Like the formula translator, it doesn't change
the state of the spreadsheet.
The procedures that print the spreadsheet on the screen are straightforward but full of details. Much of the work here goes into those details.
As we mentioned earlier, a better spreadsheet program wouldn't redraw the entire screen for each command but would change only the parts of the screen that were affected by the previous command. However, Scheme does not include a standard way to control the positioning of text on the screen, so we're stuck with this approach.
(define (print-screen) (newline) (newline) (newline) (show-column-labels (id-column (screen-corner-cell-id))) (show-rows 20 (id-column (screen-corner-cell-id)) (id-row (screen-corner-cell-id))) (display-cell-name (selection-cell-id)) (show (cell-value (selection-cell-id))) (display-expression (cell-expr (selection-cell-id))) (newline) (display "?? "))
Screen-corner-cell-id returns the ID of the cell that
should be shown in the top left corner of the display; selection-cell-id returns the ID of the selected cell.
Show-column-labels prints the first row of the display, the one with
the column letters. Show-rows is a sequential recursion that prints
the actual rows of the spreadsheet, starting with the row number of the screen-corner cell and continuing for 20 rows. (There are 30 rows in the
entire spreadsheet, but they don't all fit on the screen at once.) The rest
of the procedure displays the value and expression of the selected cell at
the bottom of the screen and prompts for the next command.
Why isn't display-expression just display?
Remember that the spreadsheet stores expressions in a form like
(+ (id 2 5) (id 6 3))
but the user wants to see
(+ b5 f3)
Display-expression is yet another tree recursion over
expressions. Just as pin-down translates cell names into cell IDs,
display-expression translates IDs back into names. (But display-expression prints as it goes along, instead of reconstructing and
returning a list.) The definition of display-expression, along with
the remaining details of printing, can be seen in the full program listing
at the end of this chapter.
Just to give the flavor of those details, here is the part that displays
the rectangular array of cell values. Show-rows is a sequential
recursion in which each invocation prints an entire row. It does so by
invoking show-row, another sequential recursion, in which each
invocation prints a single cell value.
(define (show-rows to-go col row)
(cond ((= to-go 0) 'done)
(else
(display (align row 2 0))
(display " ")
(show-row 6 col row)
(newline)
(show-rows (- to-go 1) col (+ row 1)))))
(define (show-row to-go col row)
(cond ((= to-go 0) 'done)
(else
(display (if (selected-indices? col row) ">" " "))
(display-value (cell-value-from-indices col row))
(display (if (selected-indices? col row) "<" " "))
(show-row (- to-go 1) (+ 1 col) row))))
(define (selected-indices? col row)
(and (= col (id-column (selection-cell-id)))
(= row (id-row (selection-cell-id)))))
Why didn't we write show-row in the following way?
(define (show-row to-go col row) ;; alternate version (cond ((= to-go 0) 'done) (else (let ((id (make-id col row))) (display (if (equal? id (selection-cell-id)) ">" " ")) (display-value (cell-value id)) (display (if (equal? id (selection-cell-id)) "<" " ")) (show-row (- to-go 1) (+ 1 col) row)))))
That would have worked fine and would have been a little clearer.
In fact, we did write show-row this way originally. But it's a little
time-consuming to construct an ID, and show-row is called 120 times
whenever print-screen is used. Since printing the screen was
annoyingly slow, we sped things up as much as we could, even at the cost of
this kludge.
The program keeps information about the current status of the spreadsheet
cells in a vector called *the-spreadsheet-array*. It contains all of
the 780 cells that make up the spreadsheet (30 rows of 26 columns). It's
not a vector of length 780; rather, it's a vector of length 30, each of whose
elements is itself a vector of length 26. In other words, each element of
the spreadsheet array is a vector representing one row of the spreadsheet.
(Each element of those vectors is one cell, which, as you recall, is
represented as a vector of length four. So the spreadsheet array is a
vector of vectors of vectors!)
The selectors for the parts of a cell take the cell's ID as argument and
return one of the four elements of the cell vector. Each must therefore be
implemented as two steps: We must find the cell vector, given its ID; and
we must then select an element from the cell vector. The first step is
handled by the selector cell-structure that takes a cell ID as
argument:
(define (cell-structure id)
(global-array-lookup (id-column id)
(id-row id)))
(define (global-array-lookup col row)
(if (and (<= row 30) (<= col 26))
(vector-ref (vector-ref *the-spreadsheet-array* (- row 1))
(- col 1))
(error "Out of bounds")))
Global-array-lookup makes sure the desired cell exists.
It also compensates for the fact that Scheme vectors begin with element
number zero, while our spreadsheet begins with row and column number one.
Two invocations of vector-ref are needed, one to select an entire row
and the next to select a cell within that row.
Selectors and mutators for the parts of a cell are written using
cell-structure:
(define (cell-value id) (vector-ref (cell-structure id) 0)) (define (set-cell-value! id val) (vector-set! (cell-structure id) 0 val)) (define (cell-expr id) (vector-ref (cell-structure id) 1)) (define (set-cell-expr! id val) (vector-set! (cell-structure id) 1 val)) (define (cell-parents id) (vector-ref (cell-structure id) 2)) (define (set-cell-parents! id val) (vector-set! (cell-structure id) 2 val)) (define (cell-children id) (vector-ref (cell-structure id) 3)) (define (set-cell-children! id val) (vector-set! (cell-structure id) 3 val))
The constructor is
(define (make-cell) (vector '() '() '() '()))
The spreadsheet program begins by invoking init-array to set up this
large array. (Also, it sets the initial values of the selected cell and the
screen corner.)
(define (spreadsheet)
(init-array)
(set-selection-cell-id! (make-id 1 1))
(set-screen-corner-cell-id! (make-id 1 1))
(command-loop))
(define *the-spreadsheet-array* (make-vector 30))
(define (init-array)
(fill-array-with-rows 29))
(define (fill-array-with-rows n)
(if (< n 0)
'done
(begin (vector-set! *the-spreadsheet-array* n (make-vector 26))
(fill-row-with-cells
(vector-ref *the-spreadsheet-array* n) 25)
(fill-array-with-rows (- n 1)))))
(define (fill-row-with-cells vec n)
(if (< n 0)
'done
(begin (vector-set! vec n (make-cell))
(fill-row-with-cells vec (- n 1)))))
That's the end of the project, apart from some straightforward procedures
such as letter->number that you can look up in the complete listing
if you're interested.
(define (spreadsheet)
(init-array)
(set-selection-cell-id! (make-id 1 1))
(set-screen-corner-cell-id! (make-id 1 1))
(command-loop))
(define (command-loop)
(print-screen)
(let ((command-or-formula (read)))
(if (equal? command-or-formula 'exit)
"Bye!"
(begin (process-command command-or-formula)
(command-loop)))))
(define (process-command command-or-formula)
(cond ((and (list? command-or-formula)
(command? (car command-or-formula)))
(execute-command command-or-formula))
((command? command-or-formula)
(execute-command (list command-or-formula 1)))
(else (exhibit (ss-eval (pin-down command-or-formula
(selection-cell-id)))))))
(define (execute-command command)
(apply (get-command (car command))
(cdr command)))
(define (exhibit val)
(show val)
(show "Type RETURN to redraw screen")
(read-line)
(read-line))
;;; Commands
;; Cell selection commands: F, B, N, P, and SELECT
(define (prev-row delta)
(let ((row (id-row (selection-cell-id))))
(if (< (- row delta) 1)
(error "Already at top.")
(set-selected-row! (- row delta)))))
(define (next-row delta)
(let ((row (id-row (selection-cell-id))))
(if (> (+ row delta) 30)
(error "Already at bottom.")
(set-selected-row! (+ row delta)))))
(define (prev-col delta)
(let ((col (id-column (selection-cell-id))))
(if (< (- col delta) 1)
(error "Already at left.")
(set-selected-column! (- col delta)))))
(define (next-col delta)
(let ((col (id-column (selection-cell-id))))
(if (> (+ col delta) 26)
(error "Already at right.")
(set-selected-column! (+ col delta)))))
(define (set-selected-row! new-row)
(select-id! (make-id (id-column (selection-cell-id)) new-row)))
(define (set-selected-column! new-column)
(select-id! (make-id new-column (id-row (selection-cell-id)))))
(define (select-id! id)
(set-selection-cell-id! id)
(adjust-screen-boundaries))
(define (select cell-name)
(select-id! (cell-name->id cell-name)))
(define (adjust-screen-boundaries)
(let ((row (id-row (selection-cell-id)))
(col (id-column (selection-cell-id))))
(if (< row (id-row (screen-corner-cell-id)))
(set-corner-row! row)
'do-nothing)
(if (>= row (+ (id-row (screen-corner-cell-id)) 20))
(set-corner-row! (- row 19))
'do-nothing)
(if (< col (id-column (screen-corner-cell-id)))
(set-corner-column! col)
'do-nothing)
(if (>= col (+ (id-column (screen-corner-cell-id)) 6))
(set-corner-column! (- col 5))
'do-nothing)))
(define (set-corner-row! new-row)
(set-screen-corner-cell-id!
(make-id (id-column (screen-corner-cell-id)) new-row)))
(define (set-corner-column! new-column)
(set-screen-corner-cell-id!
(make-id new-column (id-row (screen-corner-cell-id)))))
;; LOAD
(define (spreadsheet-load filename)
(let ((port (open-input-file filename)))
(sl-helper port)
(close-input-port port)))
(define (sl-helper port)
(let ((command (read port)))
(if (eof-object? command)
'done
(begin (show command)
(process-command command)
(sl-helper port)))))
;; PUT
(define (put formula . where)
(cond ((null? where)
(put-formula-in-cell formula (selection-cell-id)))
((cell-name? (car where))
(put-formula-in-cell formula (cell-name->id (car where))))
((number? (car where))
(put-all-cells-in-row formula (car where)))
((letter? (car where))
(put-all-cells-in-col formula (letter->number (car where))))
(else (error "Put it where?"))))
(define (put-all-cells-in-row formula row)
(put-all-helper formula (lambda (col) (make-id col row)) 1 26))
(define (put-all-cells-in-col formula col)
(put-all-helper formula (lambda (row) (make-id col row)) 1 30))
(define (put-all-helper formula id-maker this max)
(if (> this max)
'done
(begin (try-putting formula (id-maker this))
(put-all-helper formula id-maker (+ 1 this) max))))
(define (try-putting formula id)
(if (or (null? (cell-value id)) (null? formula))
(put-formula-in-cell formula id)
'do-nothing))
(define (put-formula-in-cell formula id)
(put-expr (pin-down formula id) id))
;;; The Association List of Commands
(define (command? name)
(assoc name *the-commands*))
(define (get-command name)
(let ((result (assoc name *the-commands*)))
(if (not result)
#f
(cadr result))))
(define *the-commands*
(list (list 'p prev-row)
(list 'n next-row)
(list 'b prev-col)
(list 'f next-col)
(list 'select select)
(list 'put put)
(list 'load spreadsheet-load)))
;;; Pinning Down Formulas Into Expressions
(define (pin-down formula id)
(cond ((cell-name? formula) (cell-name->id formula))
((word? formula) formula)
((null? formula) '())
((equal? (car formula) 'cell)
(pin-down-cell (cdr formula) id))
(else (bound-check
(map (lambda (subformula) (pin-down subformula id))
formula)))))
(define (bound-check form)
(if (member 'out-of-bounds form)
'out-of-bounds
form))
(define (pin-down-cell args reference-id)
(cond ((null? args)
(error "Bad cell specification: (cell)"))
((null? (cdr args))
(cond ((number? (car args)) ; they chose a row
(make-id (id-column reference-id) (car args)))
((letter? (car args)) ; they chose a column
(make-id (letter->number (car args))
(id-row reference-id)))
(else (error "Bad cell specification:"
(cons 'cell args)))))
(else
(let ((col (pin-down-col (car args) (id-column reference-id)))
(row (pin-down-row (cadr args) (id-row reference-id))))
(if (and (>= col 1) (<= col 26) (>= row 1) (<= row 30))
(make-id col row)
'out-of-bounds)))))
(define (pin-down-col new old)
(cond ((equal? new '*) old)
((equal? (first new) '>) (+ old (bf new)))
((equal? (first new) '<) (- old (bf new)))
((letter? new) (letter->number new))
(else (error "What column?"))))
(define (pin-down-row new old)
(cond ((number? new) new)
((equal? new '*) old)
((equal? (first new) '>) (+ old (bf new)))
((equal? (first new) '<) (- old (bf new)))
(else (error "What row?"))))
;;; Dependency Management
(define (put-expr expr-or-out-of-bounds id)
(let ((expr (if (equal? expr-or-out-of-bounds 'out-of-bounds)
'()
expr-or-out-of-bounds)))
(for-each (lambda (old-parent)
(set-cell-children!
old-parent
(remove id (cell-children old-parent))))
(cell-parents id))
(set-cell-expr! id expr)
(set-cell-parents! id (remdup (extract-ids expr)))
(for-each (lambda (new-parent)
(set-cell-children!
new-parent
(cons id (cell-children new-parent))))
(cell-parents id))
(figure id)))
(define (extract-ids expr)
(cond ((id? expr) (list expr))
((word? expr) '())
((null? expr) '())
(else (append (extract-ids (car expr))
(extract-ids (cdr expr))))))
(define (figure id)
(cond ((null? (cell-expr id)) (setvalue id '()))
((all-evaluated? (cell-parents id))
(setvalue id (ss-eval (cell-expr id))))
(else (setvalue id '()))))
(define (all-evaluated? ids)
(cond ((null? ids) #t)
((not (number? (cell-value (car ids)))) #f)
(else (all-evaluated? (cdr ids)))))
(define (setvalue id value)
(let ((old (cell-value id)))
(set-cell-value! id value)
(if (not (equal? old value))
(for-each figure (cell-children id))
'do-nothing)))
;;; Evaluating Expressions
(define (ss-eval expr)
(cond ((number? expr) expr)
((quoted? expr) (quoted-value expr))
((id? expr) (cell-value expr))
((invocation? expr)
(apply (get-function (car expr))
(map ss-eval (cdr expr))))
(else (error "Invalid expression:" expr))))
(define (quoted? expr)
(or (string? expr)
(and (list? expr) (equal? (car expr) 'quote))))
(define (quoted-value expr)
(if (string? expr)
expr
(cadr expr)))
(define (invocation? expr)
(list? expr))
(define (get-function name)
(let ((result (assoc name *the-functions*)))
(if (not result)
(error "No such function: " name)
(cadr result))))
(define *the-functions*
(list (list '* *)
(list '+ +)
(list '- -)
(list '/ /)
(list 'abs abs)
(list 'acos acos)
(list 'asin asin)
(list 'atan atan)
(list 'ceiling ceiling)
(list 'cos cos)
(list 'count count)
(list 'exp exp)
(list 'expt expt)
(list 'floor floor)
(list 'gcd gcd)
(list 'lcm lcm)
(list 'log log)
(list 'max max)
(list 'min min)
(list 'modulo modulo)
(list 'quotient quotient)
(list 'remainder remainder)
(list 'round round)
(list 'sin sin)
(list 'sqrt sqrt)
(list 'tan tan)
(list 'truncate truncate)))
;;; Printing the Screen
(define (print-screen)
(newline)
(newline)
(newline)
(show-column-labels (id-column (screen-corner-cell-id)))
(show-rows 20
(id-column (screen-corner-cell-id))
(id-row (screen-corner-cell-id)))
(display-cell-name (selection-cell-id))
(display ": ")
(show (cell-value (selection-cell-id)))
(display-expression (cell-expr (selection-cell-id)))
(newline)
(display "?? "))
(define (display-cell-name id)
(display (number->letter (id-column id)))
(display (id-row id)))
(define (show-column-labels col-number)
(display " ")
(show-label 6 col-number)
(newline))
(define (show-label to-go this-col-number)
(cond ((= to-go 0) '())
(else
(display " -----")
(display (number->letter this-col-number))
(display "----")
(show-label (- to-go 1) (+ 1 this-col-number)))))
(define (show-rows to-go col row)
(cond ((= to-go 0) 'done)
(else
(display (align row 2 0))
(display " ")
(show-row 6 col row)
(newline)
(show-rows (- to-go 1) col (+ row 1)))))
(define (show-row to-go col row)
(cond ((= to-go 0) 'done)
(else
(display (if (selected-indices? col row) ">" " "))
(display-value (cell-value-from-indices col row))
(display (if (selected-indices? col row) "<" " "))
(show-row (- to-go 1) (+ 1 col) row))))
(define (selected-indices? col row)
(and (= col (id-column (selection-cell-id)))
(= row (id-row (selection-cell-id)))))
(define (display-value val)
(display (align (if (null? val) "" val) 10 2)))
(define (display-expression expr)
(cond ((null? expr) (display '()))
((quoted? expr) (display (quoted-value expr)))
((word? expr) (display expr))
((id? expr)
(display-cell-name expr))
(else (display-invocation expr))))
(define (display-invocation expr)
(display "(")
(display-expression (car expr))
(for-each (lambda (subexpr)
(display " ")
(display-expression subexpr))
(cdr expr))
(display ")"))
;;; Abstract Data Types
;; Special cells: the selected cell and the screen corner
(define *special-cells* (make-vector 2))
(define (selection-cell-id)
(vector-ref *special-cells* 0))
(define (set-selection-cell-id! new-id)
(vector-set! *special-cells* 0 new-id))
(define (screen-corner-cell-id)
(vector-ref *special-cells* 1))
(define (set-screen-corner-cell-id! new-id)
(vector-set! *special-cells* 1 new-id))
;; Cell names
(define (cell-name? expr)
(and (word? expr)
(letter? (first expr))
(number? (bf expr))))
(define (cell-name-column cell-name)
(letter->number (first cell-name)))
(define (cell-name-row cell-name)
(bf cell-name))
(define (cell-name->id cell-name)
(make-id (cell-name-column cell-name)
(cell-name-row cell-name)))
;; Cell IDs
(define (make-id col row)
(list 'id col row))
(define (id-column id)
(cadr id))
(define (id-row id)
(caddr id))
(define (id? x)
(and (list? x)
(not (null? x))
(equal? 'id (car x))))
;; Cells
(define (make-cell)
(vector '() '() '() '()))
(define (cell-value id)
(vector-ref (cell-structure id) 0))
(define (cell-value-from-indices col row)
(vector-ref (cell-structure-from-indices col row) 0))
(define (cell-expr id)
(vector-ref (cell-structure id) 1))
(define (cell-parents id)
(vector-ref (cell-structure id) 2))
(define (cell-children id)
(vector-ref (cell-structure id) 3))
(define (set-cell-value! id val)
(vector-set! (cell-structure id) 0 val))
(define (set-cell-expr! id val)
(vector-set! (cell-structure id) 1 val))
(define (set-cell-parents! id val)
(vector-set! (cell-structure id) 2 val))
(define (set-cell-children! id val)
(vector-set! (cell-structure id) 3 val))
(define (cell-structure id)
(global-array-lookup (id-column id)
(id-row id)))
(define (cell-structure-from-indices col row)
(global-array-lookup col row))
(define *the-spreadsheet-array* (make-vector 30))
(define (global-array-lookup col row)
(if (and (<= row 30) (<= col 26))
(vector-ref (vector-ref *the-spreadsheet-array* (- row 1))
(- col 1))
(error "Out of bounds")))
(define (init-array)
(fill-array-with-rows 29))
(define (fill-array-with-rows n)
(if (< n 0)
'done
(begin (vector-set! *the-spreadsheet-array* n (make-vector 26))
(fill-row-with-cells
(vector-ref *the-spreadsheet-array* n) 25)
(fill-array-with-rows (- n 1)))))
(define (fill-row-with-cells vec n)
(if (< n 0)
'done
(begin (vector-set! vec n (make-cell))
(fill-row-with-cells vec (- n 1)))))
;;; Utility Functions
(define alphabet
'#(a b c d e f g h i j k l m n o p q r s t u v w x y z))
(define (letter? something)
(and (word? something)
(= 1 (count something))
(vector-member something alphabet)))
(define (number->letter num)
(vector-ref alphabet (- num 1)))
(define (letter->number letter)
(+ (vector-member letter alphabet) 1))
(define (vector-member thing vector)
(vector-member-helper thing vector 0))
(define (vector-member-helper thing vector index)
(cond ((= index (vector-length vector)) #f)
((equal? thing (vector-ref vector index)) index)
(else (vector-member-helper thing vector (+ 1 index)))))
(define (remdup lst)
(cond ((null? lst) '())
((member (car lst) (cdr lst))
(remdup (cdr lst)))
(else (cons (car lst) (remdup (cdr lst))))))
(define (remove bad-item lst)
(filter (lambda (item) (not (equal? item bad-item)))
lst))
25.1 The "magic numbers" 26 and 30 (and some numbers derived from them) appear many times in the text of this program. It's easy to imagine wanting more rows or columns.
Create global variables total-cols and total-rows with values 26
and 30 respectively. Then modify the spreadsheet program to refer to these
variables rather than to the numbers 26 and 30 directly. When you're done,
redefine total-rows to be 40 and see if it works.
25.2 Suggest a way to notate columns beyond z. What procedures would have
to change to accommodate this?
25.3 Modify the program so that the spreadsheet array is kept as a single vector of 780 elements, instead of a vector of 30 vectors of 26 vectors. What procedures do you have to change to make this work? (It shouldn't be very many.)
25.4 The procedures get-function and get-command are almost identical
in structure; both look for an argument in an association list. They
differ, however, in their handling of the situation in which the argument is
not present in the list. Why?
25.5 The reason we had to include the word id in each cell ID was so we
would be able to distinguish a list representing a cell ID from a list of
some other kind in an expression. Another way to distinguish cell IDs would
be to represent them as vectors, since vectors do not otherwise appear
within expressions. Change the implementation of cell IDs from
three-element lists to two-element vectors:
> (make-id 4 2) #(4 2)
Make sure the rest of the program still works.
25.6 The put command can be used to label a cell by using a quoted word
as the "formula." How does that work? For example, how is such a formula
translated into an expression? How is that expression evaluated? What if
the labeled cell has children?
25.7 Add commands to move the "window" of cells displayed on the screen without changing the selected cell. (There are a lot of possible user interfaces for this feature; pick anything reasonable.)
25.8 Modify the put command so that after doing its work it prints
14 cells modified
(but, of course, using the actual number of cells modified
instead of 14). This number may not be the entire length of a row or column
because put doesn't change an existing formula in a cell when you ask
it to set an entire row or column.
25.9 Modify the program so that each column remembers the number of digits that
should be displayed after the decimal point (currently always 2). Add a
command to set this value for a specified column. And, of course, modify
print-screen to use this information.
25.10 Add an undo command, which causes the effect of the previous command
to be nullified. That is, if the previous command was a cell selection
command, undo will return to the previously selected cell. If the
previous command was a put, undo will re-put the previous
expressions in every affected cell. You don't need to undo load or
exit commands. To do this, you'll need to modify the way the other
commands work.
25.11 Add an accumulate procedure that can be used as a function in
formulas. Instead of specifying a sequence of cells explicitly, in a
formula like
(put (+ c2 c3 c4 c5 c6 c7) c10)
we want to be able to say
(put (accumulate + c2 c7) c10)
In general, the two cell names should be taken as corners of a rectangle, all of whose cells should be included, so these two commands are equivalent:
(put (accumulate * a3 c5) d7) (put (* a3 b3 c3 a4 b4 c4 a5 b5 c5) d7)
Modify pin-down to convert the accumulate form into
the corresponding spelled-out form.
25.12 Add variable-width columns to the spreadsheet. There should be a command to set the print width of a column. This may mean that the spreadsheet can display more or fewer than six columns.
[2] Not every version of Scheme has
this behavior. If you find that you have to hit return twice after exhibiting
the value of a formula, take out one of the read-line invocations.
[3] We originally wrote two separate helper procedures for the two cases, like this:
(define (put-all-cells-in-row formula row)
(row-helper formula 1 26 row))
(define (row-helper formula this-col max-col row)
(if (> this-col max-col)
'done
(begin (try-putting formula (make-id this-col row))
(row-helper formula (+ this-col 1) max-col row))))
(define (put-all-cells-in-col formula col)
(column-helper formula 1 30 col))
(define (column-helper formula this-row max-row col)
(if (> this-row max-row)
'done
(begin (try-putting formula (make-id col this-row))
(column-helper formula (+ this-row 1) max-row col))))
but the procedures were so similar that we decided to generalize the pattern.
[4] In fact, process-command
also invokes pin-down when the user types a formula in place of a
command. In that situation, the result doesn't go into a cell but is
immediately evaluated and printed.
[5] You can
think of the cell notation in generalized formulas as a kind of
special form, but pin-down has turned those into specific cell IDs
before the formula is eligible for evaluation as an expression.
Brian Harvey,
bh@cs.berkeley.edu