
| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |

|
|
So far, the recursive procedures we've seen have all been commands, not operations. Remember that an operation is a procedure that has an output rather than an effect. In other words, an operation computes some value that is then used as the input to some other procedure. In the instruction
print first "hello
print is a command, because it does something: It prints its
input (whatever that may be) on the screen. But first is an
operation, because it computes something: With the word hello as
input, it computes the letter h, which is the first letter of
the input.
I'm going to write a program to produce secret messages. The program will take an ordinary English sentence (in the form of a Logo list) and change each letter into some other letter. For example, we can decide to replace the letter E with the letter J every time it occurs in the message. The program will need two inputs: the message and the correspondence between letters. The latter will take the form of a word of 26 letters, representing the coded versions of the 26 letters in alphabetical order. For example, the word
qwertyuiopasdfghjklzxcvbnm
indicates that the letter A in the original text will be represented by Q in the secret version, B will be represented by W, and so on.
In order to encipher a sentence, we must go through it word by word. (Strictly speaking, what we're doing is called a cipher rather than a code because the latter is a system that substitutes something for an entire word at a time, like a foreign language, whereas we're substituting for a single letter at a time, like the Elvish alphabet in The Lord of the Rings.) In order to encipher a word we must go through it letter by letter. So I'll begin by writing a procedure to translate a single letter to its coded form.
to codelet :letter :code output codematch :letter "abcdefghijklmnopqrstuvwxyz :code end to codematch :letter :clear :code if emptyp :clear [output :letter] ; punctuation character if equalp :letter first :clear [output first :code] output codematch :letter butfirst :clear butfirst :code end
Codelet is an operation that takes two inputs. The first input
must be a single-letter word, and the second must be a code, that is,
a word with the 26 letters of the alphabet rearranged. The output
from codelet is the enciphered version of the input letter. (If
the first input is a character other than a letter, such as a punctuation
mark, then the output is the same as that input.)
Codelet itself is a very simple procedure. It simply passes its
two inputs on to a subprocedure, codematch, along with another
input that is the alphabet in normal order. The idea is that
codematch will compare the input letter to each of the letters in the
regular alphabet; when it finds a match, it will output the letter in
the corresponding position in the scrambled alphabet. Be sure you
understand the use of the output command in codelet; it
says that whatever codematch outputs should become the output
from codelet as well.
The job of codematch is to go through the alphabet, letter by
letter, looking for the particular letter we're trying to encode. The
primary tool that Logo provides for looking at a single letter in a
word is first. So codematch uses first to compare
its input letter with the first letter of the input alphabet:
if equalp :letter first :clear ...
If the first input to codematch is the letter A, then
equalp will output true and codematch will output the
first letter of :code (Q in the example I gave earlier). But
suppose the first input isn't an A. Then codematch has to solve
a smaller subproblem: Find the input letter in the remaining 25
letters of the alphabet. Finding a smaller, similar subproblem means
that we can use a recursive solution. Codematch invokes itself,
but for its second and third inputs it uses the butfirsts of the
original inputs because the first letter of the alphabet (A) and its
corresponding coded letter (Q) have already been rejected.
Here is a trace of an example of codematch at work, to help you
understand what's going on.
codematch "e "abcdefghijklmnopqrstuvwxyz "qwertyuiopasdfghjklzxcvbnm
codematch "e "bcdefghijklmnopqrstuvwxyz "wertyuiopasdfghjklzxcvbnm
codematch "e "cdefghijklmnopqrstuvwxyz "ertyuiopasdfghjklzxcvbnm
codematch "e "defghijklmnopqrstuvwxyz "rtyuiopasdfghjklzxcvbnm
codematch "e "efghijklmnopqrstuvwxyz "tyuiopasdfghjklzxcvbnm
codematch outputs "t
codematch outputs "t
codematch outputs "t
codematch outputs "t
codematch outputs "t
The fifth, innermost invocation of codematch succeeds
at matching its first input (the letter E) with the first letter of
its second input. That invocation therefore outputs the first letter
of its third input, the letter T. Each of the higher-level
invocations outputs the same thing in turn.
The pattern of doing something to the first of an input, then
invoking the same procedure recursively with the butfirst as the
new input, is a familiar one from recursive commands. If we only
wanted to translate single letters, we could have written
codelet and codematch as commands, like this:
to codelet :letter :code ;; command version codematch :letter "abcdefghijklmnopqrstuvwxyz :code end to codematch :letter :clear :code ;; command version if emptyp :clear [print :letter stop] if equalp :letter first :clear [print first :code stop] codematch :letter butfirst :clear butfirst :code end
You may find this version a little easier to understand,
because it's more like the recursive commands we've examined in the
past. But making codelet an operation is a much stronger
technique. Instead of being required to print the computed code
letter, we can make that letter part of a larger computation. In
fact, we have to do that in order to encipher a complete word. Each
word is made up of letters, and the task of codeword will be to go
through a word, letter by letter, using each letter as input to
codelet. The letters output by codelet must be combined into a
new word, which will be the output from codeword.
We could write codeword using the higher order function map:
to codeword :word :code ;; using higher order function output map [codelet ? :code] :word end
But to help you learn how to write recursive operations, in this
chapter we'll avoid higher order functions. (As it turns out, map
itself is a recursive operation, written using the techniques of this
chapter.)
Recall the structure of a previous procedure that went through a word letter by letter:
to one.per.line :word if emptyp :word [stop] print first :word one.per.line butfirst :word end
Compare this to the structure of the recursive codeword:
to codeword :word :code if emptyp :word [output "] output word (codelet first :word :code) (codeword butfirst :word :code) end
There are many similarities. Both procedures have a
stop rule that tests for an empty input. Both do something to the
first of the input (either print or codelet), and each
invokes itself recursively on the butfirst of the input.
(Codeword has an extra input for the code letters, but that
doesn't really change the structure of the procedure. If that's
confusing to you, you could temporarily pretend that code is a
global variable and eliminate it as an input.)
The differences have to do with the fact that codeword is an
operation instead of a command. The stop rule invokes output
rather than stop and must therefore specify what is to be
output when the stop condition is met. (In this case, when the input
word is empty, the output is also the empty word.) But the main thing
is that the action step (the print in one.per.line) and
the recursive call (the one.per.line instruction) are not two
separate instructions in codeword. Instead they are
expressions (the two in parentheses) that are combined by word
to form the complete output. Here's a picture:
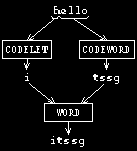
Remember what you learned in Chapter 2 about the way in
which Logo instructions are evaluated. Consider the output
instruction in codeword. Before output can be invoked,
Logo must evaluate its input. That input comes from the output from
word. Before word can be invoked, Logo must evaluate
its inputs. There are two of them. The first input to word
is the expression
codelet first :word :code
This expression computes the coded version of the first
letter of the word we want to translate. The second input to
word is the expression
codeword butfirst :word :code
This expression invokes codeword recursively, solving
the smaller subproblem of translating a smaller word, one with the
first letter removed. When both of these computations are complete,
word can combine the results to form the translation of the
complete input word. Then output can output that result.
Here's an example of how codeword is used.
? print codeword "hello "qwertyuiopasdfghjklzxcvbnm itssg
Notice that we have to say print, not just start the
instruction line with codeword; a complete instruction
must have a command. Suppose you had the idea of saving all that
typing by changing the output instruction in codeword to a
print. What would happen? The answer is that codeword
wouldn't be able to invoke itself recursively as an operation. (If
you don't understand that, try it!) Also, it's generally a better idea
to write an operation when you have to compute some result.
That way, you aren't committed to printing the result; you can use it
as part of a larger computation.
For example, right now I'd like to write a procedure code that
translates an entire sentence into code. Like codeword, it will
be an operation with two inputs, the second of which is a code (a word
of 26 scrambled letters). The difference is that the first input will
be a sentence instead of a word and the output will also be a sentence.
»Write code using a higher order function. Then see if you can
write an equivalent recursive version.
Just as codeword works by splitting up the word into letters,
code will work by splitting up a sentence into words. The
structure will be very similar. Here it is:
to code :sent :code if emptyp :sent [output []] output sentence (codeword first :sent :code) (code butfirst :sent :code) end
The main differences are that code outputs the empty
list, instead of the empty word, for an empty input and that sentence
is used as the combining operation instead of word.
Here's an example of code at work.
? print code [meet at midnight, under the dock.] ~
"qwertyuiopasdfghjklzxcvbnm
dttz qz dorfouiz, xfrtk zit rgea.
Code and codeword are examples of a very common pattern in
recursive operations: They are like using map with a particular
function. Here is the pattern that they fit.
to procedure :input if emptyp :input [output :input] output combiner (something first :input) (procedure butfirst :input) end
The combiner is often word or sentence,
although others are possible. In fact, when working with lists, the
most common combiner is not sentence but another operation that
we haven't used before, fput (First PUT). Fput takes two
inputs. The first can be any datum, but the second must be a list.
The output from fput is a list that is equal to the second
input, except that the first input is inserted as a new first member.
In other words the output from fput is a list whose first
is the first input and whose butfirst is the second input.
? show sentence [hee hee hee] [ho ho ho] [hee hee hee ho ho ho] ? show fput [hee hee hee] [ho ho ho] [[hee hee hee] ho ho ho]
Fput is a good combiner because the two things we want to
combine are the first and the butfirst of a list, except that
each has been modified in some way. But the shape of the final
result (a list of so many members) should be the same as the shape of the
input, and that's what fput ensures.
When you're working with sentences--lists of words rather than lists
of lists--sentence and fput will work equally well
as the combiner. For example, code could have been written
using fput instead of sentence. Not until some of
the later examples, when we use tree-structured lists,
will the choice really be important.
»Fput is actually a "more primitive" operation than sentence,
in the sense that the Logo interpreter actually constructs lists by
doing the internal equivalent of fput. As an exercise, you
might like to try writing your own versions of list combiners like
sentence and list out of fput, first, and
butfirst. You should also be able to write last and
butlast using only those three building blocks. (Actually you'll
also need if, emptyp, wordp, and output,
but you won't need any other primitive combiners.) Give your versions
distinct names, such as my.sentence, since Logo won't let you
redefine primitives.
»Another "less primitive" primitive is lput, an operation that
takes two inputs. As for fput, the first can be any datum but
the second must be a list. The output from lput is a list whose
last is the first input and whose butlast is the second.
Write my-lput using fput and the selectors first and
butfirst.
It may seem silly to learn a recursive pattern for problems that can be
solved using map. But sometimes we run into a problem that's
almost like a map, but not exactly. For example, how would you
write the following operation:
? show pairup [now here after glow worm hole] [nowhere hereafter afterglow glowworm wormhole]
Instead of the usual map-like situation in which each word
in the result is a function of one word of the input, this time each word of
the result is a function of two neighboring input words. Map
won't solve this problem, but the map-like recursion pattern will.
to pairup :words
if emptyp butfirst :words [output []]
output (sentence (word first :words first butfirst :words)
(pairup butfirst :words))
end
Compare this procedure with the general pattern; look for similarities and differences.
»One difference is in the test for the base case. Why is the version
in pairup different from the one in the pattern?
»Write an operation that interchanges pairs of words in a sentence, like this:
? show swap [the rain in spain stays mainly on the plain] [rain the spain in mainly stays the on plain]
Don't forget to think about that leftover word in an odd-length sentence!
Filter PatternIn Chapter 5 we saw this example:
? show filter "numberp [76 trombones, 4 calling birds, and 8 days] [76 4 8]
To write a recursive operation numbers with the same result,
we must handle three cases: the base case, in which the input is empty; the
case in which the first word of the input is a number; and the case in which
the first word isn't a number.
to numbers :sent if emptyp :sent [output []] if numberp first :sent ~ [output sentence first :sent numbers butfirst :sent] output numbers butfirst :sent end ? show numbers [76 trombones, 4 calling birds, and 8 days] [76 4 8]
Here's the general filter pattern:
to procedure :input if emptyp :input [output :input] if predicate first :input ~ [output combiner first :input procedure butfirst :input] output procedure butfirst :input end
As in the case of the map pattern, this one is most useful
in situations for which the higher order function won't quite do.
»Write an operation that looks for two equal words next to each other in a sentence, and outputs a sentence with one of them removed:
? show unique [Paris in the the spring is a joy joy to behold.] Paris in the spring is a joy to behold.
What does your procedure do with three consecutive equal words? What should it do?
Reduce PatternOther examples from Chapter 5 introduced the reduce higher
order function.
? show reduce "word [C S L S] CSLS ? show reduce "sum [3 4 5 6] 18
Recursive operations equivalent to these examples are very much
like the map pattern except that the combiner function is applied to
the members of the input directly, rather than to some function of the
members of the input:
to wordify :sentence if emptyp :sentence [output "] output word (first :sentence) (wordify butfirst :sentence) end to addup :numbers if emptyp :numbers [output 0] output sum (first :numbers) (addup butfirst :numbers) end
What are the differences between these two examples? There are two: the combiner used and the value output in the base case. Here is the pattern:
to procedure :input if emptyp :input [output identity] output combiner (first :input) (procedure butfirst :input) end
The identity in this pattern depends on the combiner; it's
the value that, when combined with something else, gives that something else
unchanged as the result. Thus, zero is the identity for sum, but the
identity for product would be one.
»Write a multiply operation that takes a list of numbers as its
input and returns the product of all the numbers.
»You can make your multiply procedure more efficient, in some
situations, by having it notice when one of the numbers in the input list is
zero. In that case, you can output zero as the overall result without
looking at any more numbers. The resulting procedure will, in a sense,
combine aspects of the filter and reduce patterns.
Addup is one example of an important sub-category of reduce-like
procedures in which the "combining"
operation is arithmetic, usually sum. The simplest example is a
procedure equivalent to the primitive count, which counts the
members of a list or the letters of a word:
to length :thing if emptyp :thing [output 0] output 1+length butfirst :thing end
In this procedure, as usual, we can see the reduction of a
problem to a smaller subproblem. The length of any word or list is
one more than the length of its butfirst. Eventually this
process of shortening the input will reduce it to emptiness; the
length of an empty word or list is zero.
Although count is a primitive, there are more complicated
counting situations in which not every member should be counted. For
example, here is a procedure to count the number of vowels in a word:
to vowelcount :word if emptyp :word [output 0] if vowelp first :word [output 1+vowelcount butfirst :word] output vowelcount butfirst :word end to vowelp :letter output memberp :letter [a e i o u] end
(Actually, my predicate vowelp is somewhat
oversimplified. The letter Y is a vowel in certain positions in the
word, and even some other letters can sometimes play the role of a
vowel. But this isn't a book on linguistics!)
You can see the similarities between vowelcount and
length. The difference is that, in effect, length uses a
predicate that is always true, so it always carries out the
instruction inside the if. Here's the pattern:
to procedure :input if emptyp :input [output 0] if predicate first :input [output 1+procedure butfirst :input] output procedure butfirst :input end
»Try writing a procedure that will accept as
input a word like 21,997.00 and output the number of digits
before the decimal point. (In this case the correct output is 5.)
Don't assume that there is a decimal point; your program
shouldn't blow up no matter what word it gets as input.
»Another counting problem is to output the position of a member in a
list. This operation is the inverse to item, a Logo primitive,
which outputs the member at a given position
number. What I'm asking you to write is index, which works like
this:
? print index "seven [four score and seven years ago] 4 ? print index "v "aardvark 5
Find Pattern
A variation of the filter pattern
is for selection operations: ones that pick a single element out of a
list. The general idea looks like this:
to procedure :input if emptyp :input [output :input] if predicate first :input [output something first :input] output procedure butfirst :input end
There will generally be extra inputs to these procedures, to indicate the basis for selection. For example, here is a program that translates English words into French.
to french :word output lookup :word [[book livre] [computer ordinateur] [window fenetre]] end to lookup :word :dictionary if emptyp :dictionary [output "] if equalp :word first first :dictionary [output last first :dictionary] output lookup :word butfirst :dictionary end ? print french "computer ordinateur
The expression
first first :dictionary
selects the English word from the first word-pair in the list. Similarly,
last first :dictionary
selects the French version of the same word. (Of course, in
reality, the word list in french would be much longer than the
three word-pairs I've shown.)
Codematch, in the example that started this chapter, follows
the same pattern of selection. The only difference is that there are
two inputs that are butfirsted in parallel.
Somewhat similar to the selection pattern is one for a recursive predicate; the difference is that instead of
output something first :input
for a successful match, the procedure simply says
output "true
in that case. This pattern is followed by predicates that ask a question like "Does any member of the input do X?" For example, suppose that instead of counting the vowels in a word, we just want to know whether or not there is a vowel. Then we're asking the question "Is any letter in this word a vowel?" Here's how to find out.
to hasvowelp :word if emptyp :word [output "false] if vowelp first :word [output "true] output hasvowelp butfirst :word end
A more realistic example is also somewhat more cluttered with extra
inputs and sometimes extra end tests. Here's a procedure that takes
two words as input. It outputs true if the first word comes
before the second in the dictionary.
to sort.beforep :word1 :word2 if emptyp :word1 [output "true] if emptyp :word2 [output "false] if (ascii first :word1) < (ascii first :word2) [output "true] if (ascii first :word1) > (ascii first :word2) [output "false] output sort.beforep butfirst :word1 butfirst :word2 end
The procedure will end on one of the emptyp tests if
one of the input words is the beginning of the other, like now
and nowhere. Otherwise, the procedure ends when two letters are
unequal. The recursion step is followed when the beginning letters
are equal. (The operation ascii takes a one-character word as
input, and outputs the numeric value for that character in the computer's
coding system, which is called the American Standard Code for Information
Interchange.)
A combination of the translation kind of operation and the selection
kind is an operation that selects not one but several members of the
input. For example, you sometimes want to examine the words in a
sentence in various ways but have trouble because the sentence
includes punctuation as part of some words. But the punctuation isn't
really part of the word. In Chapter 4, for instance, I
defined a predicate about.computersp and gave this example of
its use:
? print about.computersp [this book is about programming] true
But if the example were part of a larger program, carrying
on a conversation with a person, the person would probably have ended
the sentence with a period. The last word would then have been
programming. (including the period). That word, which is
different from programming without the period, isn't in the
procedure's list of relevant words, so it would have output false.
The solution is to write a procedure that strips the punctuation from
each word of a sentence. Of course that's a straightforward case of
the translation pattern, applying a subprocedure to each word of the
sentence:
to strip :sent if emptyp :sent [output []] output sentence (strip.word first :sent) (strip butfirst :sent) end
Strip.word, though, is more interesting. It must
select only the letters from a word.
to strip.word :word
if emptyp :word [output "]
if letterp first :word ~
[output word (first :word) (strip.word butfirst :word)]
output strip.word butfirst :word
end
to letterp :char
output or (inrangep (ascii :char) (ascii "A) (ascii "Z)) ~
(inrangep (ascii :char) (ascii "a) (ascii "z))
end
to inrangep :this :low :high
output and (:this > (:low-1)) (:this < (:high+1))
end
Strip.word is like the translation pattern in the use
of the combining operation word in the middle instruction line.
But it's also like the selection pattern in that there are two
different choices of output, depending on the result of the predicate
letterp.
»You might want to rewrite about.computersp so that it uses
strip. Consider an initialization procedure.
Cascade PatternCertain mathematical functions are defined in terms of recursive calculations. It used to be that computers were used only for numerical computation. They're now much more versatile, as you've already seen, but sometimes the old numerical work is still important.
The classic example in this category is the factorial function. The factorial of a positive integer is the product of all the integers from 1 up to that number. The factorial of 5 is represented as 5! so
We can use cascade to carry out this computation:
to fact :n ;; cascade version output cascade :n [? * #] 1 end ? print fact 5 120
In this example I'm using a feature of cascade that we
haven't seen before. The template (the second input to cascade) may
include a number sign (#) character, which represents the number of
times the template has been repeated. That is, it represents 1 the first
time, 2 the second time, and so on.
Here is a recursive version of fact that takes one input, a
positive integer, and outputs the factorial function of that number.
The input can also be zero; the rule is that 0!=1.
to fact :n if :n=0 [output 1] output :n * fact :n-1 end
This procedure works because
That's another version of reducing a problem to a smaller subproblem.
»Chapter 5 gives the following example:
to power :base :exponent output cascade :exponent [? * :base] 1 end
Write a version of power using recursion instead of using
cascade.
Another classic example, slightly more complicated, is the Fibonacci sequence. Each number in the sequence is the sum of the two previous numbers; the first two numbers are 1. So the sequence starts
A formal definition of the sequence looks like this:
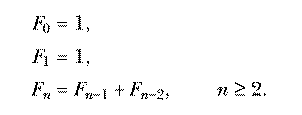
Here's an operation fib
that takes a number n as input and outputs Fn.
to fib :n if :n<2 [output 1] output (fib :n-1)+(fib :n-2) end
That procedure will work, but it's quite seriously
inefficient. The problem is that it ends up computing the same
numbers over and over again. To see why, here's a trace of what
happens when you ask for fib 4:
fib 4
fib 3
fib 2
fib 1
fib 0
fib 1
fib 2
fib 1
fib 0
Do you see the problem? fib 2 is computed twice, once
because fib 4 needs it directly and once because fib 4
needs fib 3 and fib 3 needs fib 2. Similarly,
fib 1 is computed three times. As the input to fib gets
bigger, this problem gets worse and worse.
It turns out that a much faster way to handle this problem is to compute a list of all the Fibonacci numbers up to the one we want. Then each computation can take advantage of the work already done. Here's what I mean:
to fiblist :n if :n<2 [output [1 1]] output newfib fiblist :n-1 end to newfib :list output fput (sum first :list first butfirst :list) :list end ? print fiblist 5 8 5 3 2 1 1
We can then define a faster fib in terms of
fiblist:
to fib :n output first fiblist :n end
Convince yourself that the two versions of fib give
the same outputs but that the second version is much faster. I'm
purposely not going through a detailed explanation of this example;
you should use the analytical techniques you learned in Chapter 8.
What problem is fiblist trying to solve? What is the smaller
subproblem?
The hallmark of numerical recursion is something like :n-1 in the
recursion step. Sometimes this kind of recursion is combined with the
butfirst style we've seen in most of the earlier examples. Logo has a
primitive operation called item, which takes two inputs. The first is
a positive integer, and the second is a list. The output from item is
the nth member of the list if the first input is n. (Earlier
I suggested that you write index, the opposite of item.) If Logo
didn't include item, here's how you could write it:
to item :n :list if equalp :n 1 [output first :list] output item :n-1 butfirst :list end
When I was growing up, every kid learned a not-very-secret "secret" language called Pig Latin. When I became a teacher, I was surprised to find out that kids apparently didn't learn it any more. But more recently it seems to have come back into vogue. Translating a sentence into Pig Latin is an interesting programming problem, so I'm going to teach it to you.
Here's how it works. For each word take any consonants that are at the beginning (up to the first vowel) and move them to the end. Then add "ay" at the end. So "hello" becomes "ellohay"; "through" becomes "oughthray"; "aardvark" just becomes "aardvarkay." (Pig Latin is meant to be spoken, not written. You're supposed to practice so that you can do it and understand it really fast.)
By now you can write in your sleep the operation
piglatin, which
takes a sentence and outputs its translation into Pig Latin by going
through the sentence applying a subprocedure plword to each
word. (It's just like code, only different.)
It's plword that is the tricky part. The stop rule is
pretty straightforward:
if vowelp first :word [output word :word "ay]
If the first letter isn't a vowel, what we want to do is move that letter to the end and try again. Here's the complete procedure.
to plword :word if vowelp first :word [output word :word "ay] output plword word butfirst :word first :word end
What makes this tricky is that the recursion step doesn't seem to make the problem smaller. The word is still the same length after we move the first letter to the end. This would look more like all the other examples if the recursion step were
output plword butfirst :word
That would make the procedure easier to understand. Unfortunately it would also give the wrong answer. What you have to see is that there is something that is getting smaller about the word, namely the "distance" from the beginning of the word to the first vowel. Trace through a couple of examples to clarify this for yourself.
By the way, this will work better if you modify vowelp (which we
defined earlier) so that y is considered a vowel. You'll then
get the wrong answer for a few strange words like yarn, but on
the other hand, if you consider y a consonant, you'll get no
answer at all for words like try in which y is the only
vowel! (Try it. Do you understand what goes wrong?)
»Some people learned a different dialect of Pig Latin. According to
them, if the word starts with a vowel in the first place, you should
add "way" at the end instead of just "ay." Modify plword so
that it speaks that dialect. (I think the idea is that some words
simply sound better with that rule.) Hint: You'll want an
initialization procedure.
»The top-level procedure piglatin, which you wrote yourself, is a
good candidate for careful thought about punctuation. You don't want
to see
? print piglatin [what is he doing?] atwhay isway ehay oing?day
A good first attempt would be to modify piglatin to
use strip, to get rid of the punctuation altogether. But even
better would be to remove the punctuation from each word, translate it
to Pig Latin, then put the punctuation back! Then we could get
atwhay isway ehay oingday?
That's the right thing to do for punctuation at the end of a
word, like a period or a comma. On the other hand, the apostrophe
inside a word like isn't should be treated just like a letter.
The project I'm proposing to you is a pretty tricky one. Here's a
hint. Write an operation endpunct that takes a word as input
and outputs a list of two words, first the "real" word
full of letters, then any punctuation that might be at the end. (The
second word will be empty if there is no such punctuation.) Then your
new plword can be an initialization procedure that invokes a
subprocedure with endpunct's output as its input.
Write a procedure number.name that takes a positive integer
input, and outputs a sentence containing that number spelled out in words:
? print number.name 5513345 five million five hundred thirteen thousand three hundred forty five ? print number.name (fact 20) two quintillion four hundred thirty two quadrillion nine hundred two trillion eight billion one hundred seventy six million six hundred forty thousand
There are some special cases you will need to consider:
Here are two hints. First, split the number into groups of three digits, going from right to left. Also, use the sentence
[thousand million billion trillion quadrillion quintillion sextillion septillion octillion nonillion decillion]
You can write this bottom-up or top-down. To work bottom-up, pick a subtask
and get that working before you tackle the overall structure of the
problem. For example, write a procedure that returns the word fifteen
given the argument 15.
To work top-down, start by writing number.name, freely assuming the
existence of whatever helper procedures you like. You can begin debugging
by writing stub procedures that fit into the overall program but
don't really do their job correctly. For example, as an intermediate stage
you might end up with a program that works like this:
? print number.name 1428425 ;; intermediate version 1 million 428 thousand 425
SubsetsWe've seen that recursive operations can do the same jobs as higher order functions, and we've seen that recursive operations can do jobs that are similar to the higher order function patterns but not quite the same. Now we'll see that recursive operations can do jobs that are quite outside the bounds of any of the higher order functions in Chapter 5.
I'd like to write an operation subsets that takes a word as input.
Its output will be a sentence containing all the words that can be made
using letters from the input word, in the same order, but not necessarily
using all of them. For example, the word lit counts as a subset of
the word lights, but hit doesn't count because the letters are
in the wrong order. (Of course the procedure won't know which words are
real English words, so iht, which has the same letters as hit
in the right order, does count.)
»How many subsets does lights have? Write them all down if
you're not sure. (Or perhaps you'd prefer to count the subsets of a shorter
word, such as word, instead.)
A problem that follows the map pattern is one in which the size of the
output is the same as the size of the input, because each member of the
input gives rise to one member of the output. A problem that follows the
filter pattern is one in which the output is smaller than the input,
because only some of the members are selected. And the reduce pattern
collapses all of the members of the input into one single result. The
subsets problem is quite different from any of these; its output will
be much larger than its input.
If we can't rely on known patterns, we'll have to go back to first
principles. In Chapter 8 you learned to write recursive procedures by
looking for a smaller, similar subproblem within the problem we're trying to
solve. What is a smaller subproblem that's similar to finding the subsets
of lights? How about finding the subsets of its butfirst? This idea
is the same one that's often worked for us before. So imagine that we've
already found all the subsets of ights.
Some of the subsets of lights are subsets of ights.
Which ones aren't? The missing subsets are the ones that start with the
letter L. What's more, the other letters in such a subset form a subset of
ights. For example, the word lits consists of the letter L
followed by its, which is a subset of ights.
to subsets :word ;; incomplete local "smaller make "smaller subsets butfirst :word output sentence :smaller (map [word (first :word) ?] :smaller) end
This procedure reflects the idea I've just tried to explain. The subsets of a given word can be divided into two groups: the subsets of its butfirst, and those same subsets with the first letter of the word stuck on the front.
The procedure lacks a base case. It's tempting to say that if the input is
an empty word, then the output should be an empty sentence. But that isn't
quite right, because every word is a subset of itself, so in particular the
empty word is a subset (the only subset) of itself. We must output a
sentence containing an empty word. That's a little tricky to type, but we
can represent a quoted empty word as " and so a sentence containing an
empty word is (sentence ").
to subsets :word if emptyp :word [output (sentence ")] local "smaller make "smaller subsets butfirst :word output sentence :smaller (map [word (first :word) ?] :smaller) end
Why did I use the local variable smaller and a make
instruction? It wasn't strictly necessary; I could have said
output sentence (subsets butfirst :word) ~
(map [word (first :word) ?] (subsets butfirst :word))
The trouble is that this would have told Logo to compute the smaller similar subproblem twice instead of just once. It may seem that that would make the program take twice as long, but in fact the problem is worse than that, because each smaller subproblem has a smaller subproblem of its own, and those would be computed four times--twice for each of the two computations of the first smaller subproblem! As in the case of the Fibonacci sequence we studied earlier, avoiding the duplicated computation makes an enormous difference.
Problems like this one, in which the size of the output grows extremely
quickly for small changes in the size of the input, tend to be harder to
program than most. Here are a couple of examples. Like subsets, each
of these has a fairly short procedure definition that hides a very complex
computation.
»On telephone dials, most digits have letters associated with them. In the United States, for example, the digit 5 is associated with the letters J, K, and L. (The correspondence is somewhat different in other countries.) You can use these letters to spell out words to make your phone number easier to remember. For example, many years ago I had the phone number 492-6824, which spells I-WANT-BH. Write a procedure that takes a number as its input, and outputs a sentence of all the words that that number can represent. You may want to test the program using numbers of fewer than seven digits!
»In the game of BoggleTM, the object is to find words by connecting neighboring letters in a four by four array of letters. For example, the array
BEZO URND AKAJ WEOE
contains the words ZEBRA, DONE, and DARK, but not RADAR, because
each letter can be used only once. Write a predicate procedure that takes a
word and an array of letters (in the form of a sentence with one word for
each row) as inputs, and outputs true if and only if the given word
can be found in the given array.
? print findword "zebra [bezo urnd akaj weoe] true ? print findword "radar [bezo urnd akaj weoe] false
What I want to talk about in the rest of this chapter isn't really very important, so you can skip it if you want. But some people think it's important, so this is for those people.
Every procedure invocation takes up a certain amount of computer memory, while the procedure remains active, to hold things like local variables. Since a recursive procedure can invoke itself many times, recursion is a fairly "expensive" technique to allow in a programming language. It turns out that if the only recursion step in a procedure is the very last thing the procedure does, the interpreter can handle that procedure in a special way that uses memory more efficiently. You can then use as many levels of recursive invocation as you want without running out of space. Such a procedure is called tail recursive. It doesn't make any difference to you as a programmer; it's just a matter of what's happening inside the Logo interpreter.
A tail recursive command is very easy to recognize; the last instruction is an invocation of the same procedure. Tail recursive commands are quite common; here are a couple of examples we've seen before.
to one.per.line :thing if emptyp :thing [stop] print first :thing one.per.line butfirst :thing end to poly :size :angle forward :size right :angle poly :size :angle end
The thing is, many people are confused about what constitutes a tail
recursive operation. It isn't one that is invoked
recursively on the last instruction line! Instead, the rule is that
the recursive invocation must be used directly as the input
to output, not as part of a larger computation. For example,
this is a tail recursive operation:
to lookup :word :dictionary if emptyp :dictionary [output "] if equalp :word first first :dictionary [output last first :dictionary] output lookup :word butfirst :dictionary end
But this is not tail recursive:
to length :thing if emptyp :thing [output 0] output 1+length butfirst :thing end
It's that 1+ that makes the difference.
It's sometimes possible to change a nontail recursive operation into
a tail recursive one by tricky programming. For example, look again
at fact:
to fact :n if :n=0 [output 1] output :n * fact :n-1 end
This is not tail recursive because the input to the final
output comes from the multiplication, not directly from
fact. But here is a tail recursive version:
to fact :n output fact1 :n 1 end to fact1 :n :product if :n=0 [output :product] output fact1 (:n-1) (:n*:product) end
Indeed, this version can, in principle, compute the factorial of larger numbers than the simpler version without running out of memory. In practice, though, the largest number that most computers can understand is less than the factorial of 70, and any computer will allow 70 levels of recursion without difficulty. In fact, not every Logo interpreter bothers to recognize tail recursive operations. It's a small point; I only mention it because some people both make a big fuss about tail recursion and misunderstand what it means!
Brian Harvey,
bh@cs.berkeley.edu