
| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |

|
|
Program file for this chapter: playfair
This project investigates a cipher that is somewhat more complicated than the simple substitution cipher of Chapter 11. In the Playfair cipher, there is not a single translation of each letter of the alphabet; that is, you don't just decide that every B will be turned into an F. Instead, pairs of letters are translated into other pairs of letters.
Here is how it works. To start, pick a keyword that does not
contain any letter more than once. For example, I'll pick the word
keyword. Now write the letters of that word in the first squares of a
five by five matrix:
| K | E | Y | W | O |
| R | D | |||
Then finish filling up the remaining squares of the matrix with the remaining letters of the alphabet, in alphabetical order. Since there are 26 letters and only 25 squares, we assign I and J to the same square.
| K | E | Y | W | O |
| R | D | A | B | C |
| F | G | H | I J | L |
| M | N | P | Q | S |
| T | U | V | X | Z |
(Actually, when choosing the keyword, besides making sure that no
letter appears twice you must make sure that I and J do not both appear.
For example, juice wouldn't do as a keyword.)
To encipher a message, divide it into pairs of letters. Pay no attention to punctuation or to spaces between words. For example, the sentence "Why, don't you?" becomes
WH YD ON TY OU
Now, find each pair of letters in the matrix you made earlier.
Most pairs of letters will form two corners of a smaller square or rectangle
within the matrix. For example, in my matrix, the first pair of letters
(WH) are at two corners of a two-by-three rectangle also containing
Y, A, B, and IJ. The enciphering of the pair
WH is the pair at the two other corners of this rectangle, namely
YI. (I could also have chosen YJ, in this case.) It's important to
be consistent about the order of the new pair: the one that comes first is
the one on the same row as the first of the original pair. In this
case, Y is on the same row as W. We can continue to translate
the remaining pairs of letters in the same way, ending up with
YI EA ES VK EZ
Notice that the letter Y turned into E in the second
pair of letters, but it turned into K in the fourth pair.
Part of the strategy for keeping a code secret is to hide even the kind of code being used. Pairs of letters, to a cryptographer, are a dead giveaway that a Playfair cipher was used, so it's traditional to insert irrelevant spacing and punctuation in the actual written version of the message, like this:
Yie ae, svkez.
Of course the recipient of the message, knowing how the message was encoded, ignores this spacing and punctuation.
As an illustration of some of the special cases that complicate this scheme, consider the message, "Come to the window." First we divide it up into pairs:
CO ME TO TH EW IN DO W
The first problem is that the message has an odd number of
letters. To solve this problem we simply add an extra letter at the end,
generally Q. In this example, the final W becomes a pair
WQ.
If you look up the first pair of letters, CO, in my matrix, you'll
find that they do not determine a rectangle, because they are in the same
column. (Strictly speaking, they do determine a one-by-two
rectangle, but the two diagonals are the same, so that CO would be
encoded as CO if we followed the usual rule.) For two letters in the
same column, the rule is to replace each letter by the one below it, so
CO becomes LC. (If one of the letters is at the end of the column,
it is replaced by the top letter. So, for example, OZ would become
CO.) Similarly, for two letters in the same row, each is replaced by
the letter to its right. We can now translate the entire message:
LC NK ZK VF YO GQ CE BX
The pair EW, on a single row, has become YO; the final
pair WQ, on a single column, has become BX.
The final exceptional case is the one in which the same letter appears twice in a pair. For example, the phrase "the big wheel" divides into
TH EB IG WH EE LQ
The pair EE is treated specially. It could be translated
into YY (treating it as two letters in the same row) or into DD
(if you think of it as two letters in the same column). Instead, though,
the rule is to break up the pair by inserting a Q between the two
letters. This changes all the pairings after that one in the message. The
new version is
TH EB IG WH EQ EL
This version can now be translated into
VF WD LH YJ WN OG
(Notice that I chose to translate WH into YJ instead of into
YI. You should use some of each when coding a message. A cipher with
no Js at all, or one with a simple pattern of I and J
alternating, is another giveaway that the Playfair cipher was used.)
What about the frequencies of letters in a Playfair-encoded message? You
can't simply say that the most common letters are likely to represent
E or T or A, because a letter doesn't represent a single letter
that way. But it is still possible to say that a common letter in the coded
version is likely to be on the same row as one of the frequent
letters in English. For example, here is a well-known text
in Playfair-coded form:
ZK DW KC SE XM ZK DW VF RV LQ VF WN ED MZ LW QE GY VF KD XF MP WC GO BF MU GY QF UG ZK NZ IM GK FK GY ZS GQ LN DP AB BM CK OQ KL EZ KF DH YK ZN LK FK EU YK FK KZ RY YD FT PC HD GQ MZ CP YD KL KF EZ CI ON DP AC WK QS SY QL UN DU RU GY NS
The most commonly occurring letters in this coded text are K
(19 times), F (12 times), D and Z (tied at 11), and
Y (10 times). K is on the same row as both E and O, and
can also represent T in the same-column case. Y is also on the
same row. F can represent I (especially in the common pair
IT); D can represent A; Z can represent T. Of all
the letters that might represent E, why should K and Y be
the popular ones? The answer is that they have common letters in their
columns as well. In order for W to represent E, for example,
the other letter of the (cleartext) pair must be B, I, J,
Q, or X. Of these, only I is particularly common, and
Q and X are downright rare.
If you were trying to break a Playfair cipher, one approach you might take
would be to count the frequencies of pairs of letters. For example,
in the message above, the only pairs that occur more than twice are
GY, four times, and FK, VF, and ZK, three times each.
It's a good guess that each of these corresponds to a commonly occurring
pair of letters in English text. In fact, as it turns out, GY
corresponds to HE, which is not only a word by itself but also part of
the, them, then, and so on. VF corresponds to
TH, an extremely common pair; ZK corresponds to TO, which is
again a word in itself as well as a constituent of many other words. The
other pair that occurs three times in the text, FK, corresponds to
RT. This is not such a common English pair, although it does come up
in words like worth. But it turns out that in the particular sample
text I'm using, this pair of letters comes up mostly as parts of two words,
as in the combination or to.
If you want to know more about how to break a Playfair cipher, you can see
an example in Have His Carcase, a mystery novel by
Dorothy L. Sayers. In this project, I'm less ambitious: the
program merely enciphers a message, given the keyword and the cleartext as
inputs. The first input to playfair must be a word, the keyword. The
second input must be a list of words, the text. The keyword must meet the
criterion of no duplicated letters, and the cleartext input must contain
only words of letters, without punctuation. Here is an example:
? print playfair "keyword [come to the window] lcnkzkvfyogqcebx
Playfair is an operation whose output is a single word
containing the enciphered letters of the original text.
In writing this program, the first question I thought about was how to
represent in a Logo program the matrix of letters used in the coding
process. The most natural structure is a two-dimensional array--that is,
an array with five members, each of which is an array of five
letters.* So if
the keyword is keyword then the program will, in effect, do this:
*In the tic-tac-toe program, I used a one-dimensional array
to represent the board, even though a tic-tac-toe board is drawn in two
dimensions. I could have used an array of three arrays of three numbers
each, but that wouldn't really have fit with the way that program labels the
board. In tic-tac-toe, the nine squares are named 1 to 9. You ask to move
in square 8, for example, not in row 3, column 2. But in the Playfair
program, the row and column numbers are going to be very important.
make "matrix {{k e y w o} {r d a b c} {f g h i l}
{m n p q s} {t u v x z}}
The position of a letter in the matrix is represented as a list of
two numbers, the row and the column. The Berkeley Logo procedure library
includes an operation mditem that takes such a list as an input, along
with a multi-dimensional array, and outputs the desired member:
to letter :rowcol output mditem :rowcol :matrix end
(The actual procedure listed at the end of this section includes a
slight complication to deal with the case of I and J, but that's
not important right now.)
The Playfair process goes like this: The program is given two letters. It
finds each letter in the matrix, determines each letter's row and column
numbers, then rearranges those numbers to make new row and column numbers,
then looks in the matrix again to find the corresponding letters. For
example, suppose we are given the keyword keyword and the letters
T and A. The first step is to translate T into the row and
column list [5 1], and to translate A into [2 3]. Then
the program must combine the row of one letter with the column of the other,
giving the new lists [5 3] and [2 1]. Finally, the letter
procedure shown above will find the letters V and R in the
matrix.
Letter handles the last step of the translation process, but what about
the first step? We need the inverse operation of letter, one that
takes a letter as input and provides its row and column.
It would be possible to write a row.and.column procedure that would
examine each letter in the matrix until it located the desired letter. But
that procedure would be both slow and complicated. Instead, I decided
to keep redundant information about the matrix in the form of 26
variables, one for each letter, each of which contains the coordinates of
that letter. That is, the variables take the form
make "a [2 3] make "w [1 4] make "z [5 5]
and so on. (As in the case of the variable named matrix
above, these make instructions are just illustrative. The actual
program does not contain explicit data for this particular matrix, using
this particular keyword!)
The letter variables contain the same information as the variable
matrix. Strictly speaking, they are not needed. By creating the redundant
variables for the letters, I've made a space/time tradeoff;
the extra variables take up room in the computer's memory, but the program
runs faster. One of the recurring concerns of a professional programmer is
deciding which way to make such tradeoffs. It depends on the amounts of
space and time required and the amounts available. In this case, the extra
space required is really quite small, compared to the memory of a modern
computer, so the decision is clear-cut. For larger programming problems it
is sometimes harder to decide.
Earlier I showed a make instruction to put a particular coding matrix
into the variable matrix. How does the program create a matrix for
any keyword given as input? Here are two of the relevant procedures:
to playfair :keyword :message local [matrix a b c d e f g h i j k l m n o p q r s t u v w x y z] setkeyword jtoi lowercase :keyword output encode (reduce "word :message) end to setkeyword :word make "matrix reorder word :word (remove :word "abcdefghiklmnopqrstuvwxyz) make "j :i end
The keyword that is provided by the user as one of the inputs to the
toplevel procedure playfair goes through several stages as it is
transformed into a matrix.
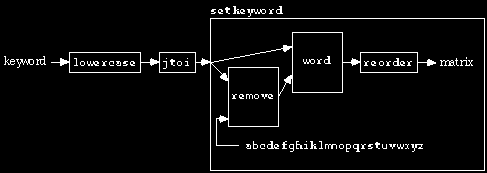
This dataflow diagram is very similar to a plumbing diagram from Chapter 2 turned on its side. The format is a little different to put somewhat more emphasis on the inputs and outputs, so you can follow the "flow" of information through the arrows.
In English, here's what the diagram tells us. The keyword given by the user
must be converted to lower case letters. (I could have chosen to use capital
letters instead; the goal is to have some uniform convention.) If the
keyword happens to contain a J, it will be represented within the
program as an I instead. Then, to make the matrix, we combine (with
word) two words: the keyword and the result of removing the keyword's
letters from the alphabet (leaving out J). Finally, that combined
word must be rearranged into a five-by-five square.
The advantage of a view such as this one is that each of the small boxes
in the diagram has a relatively simple task. Indeed, lowercase and
word are primitive operations in Berkeley Logo. Jtoi is trivial:
to jtoi :word output map [ifelse equalp ? "j ["i] [?]] :word end
Remove is a straightforward recursive operation that
outputs the result of removing one group of letters from another group
of letters.
to remove :letters :string if emptyp :string [output "] if memberp first :string :letters [output remove :letters bf :string] output word first :string remove :letters bf :string end
The job of reorder is somewhat messier. It must keep track
of what row and column it's up to, so reorder is just an
initialization procedure for the recursive helper reorder1 that does
the real work. Reorder also creates the two-dimensional Logo array
to provide another input to its helper procedure.
to reorder :string output reorder1 :string (mdarray [5 5]) 1 1 end to reorder1 :string :array :row :column if :row=6 [output :array] if :column=6 [output reorder1 :string :array :row+1 1] mdsetitem (list :row :column) :array first :string make first :string (list :row :column) output reorder1 (butfirst :string) :array :row :column+1 end
If I were filling in a matrix by hand, instead of writing a computer
program, I'd use a very different approach. I'd handle one letter at a
time. First I'd go through the keyword a letter at a time, stuffing each
letter into the next available slot in the matrix. (If necessary, I'd
convert upper to lower case and J to I in the process.)
Then I'd go through the alphabet a letter at a time, saying "If this letter
isn't in the keyword, then stuff it into the matrix."
Many people would find it natural to use that same technique in writing a computer program, also:
to playfair :keyword :message ;; sequential version
local [matrix a b c d e f g h i j k l m n o p q r s t u v w x y z]
make "matrix mdarray [5 5]
local [row column]
make "row 1
make "column 1
foreach :keyword [stuff jtoi lowercase ?]
foreach "abcdefghiklmnopqrstuvwxyz ~
[if not memberp ? jtoi :keyword [stuff ?]]
make "j :i
output encode (reduce "word :message)
end
to stuff :letter
mdsetitem (list :row :column) :matrix :letter
make :letter (list :row :column)
make "column :column+1
if :column=6 [make "row :row+1 make "column 1]
end
In this version, the first foreach instruction handles the letters of
the keyword. The second foreach instruction handles the rest of the
alphabet. The not memberp test handles the removal of the keyword
letters from the alphabet.
My intent in writing this alternate version was to model my idea of how the problem would be solved without a computer, processing one letter at a time. So, for example, in the template
[stuff jtoi lowercase ?]
it's worth noting that the operations jtoi and
lowercase are being applied to single-letter inputs, even though those
operations were designed to accept words of any length as a unit. I
cheated, though, by applying jtoi to the entire keyword in the
second foreach instruction. I was trying to make the program more
readable; the honest version would be
foreach "abcdefghiklmnopqrstuvwxyz ~
[if (ifelse equalp ? "i
[not (or (memberp "i :keyword)
(memberp "j :keyword))]
[not memberp ? :keyword])
[stuff ?]]
Why am I subjecting you to this? My point is that what may seem to be the most natural way to think about a problem--in this case, handling one letter at a time--may not be the easiest, most elegant, or most efficient programming solution.
What makes the dataflow-structured version of playfair possible is the
use of operations in Logo, and the composition of these
operations by using the output from one as the input to another. This is an
important technique, but one that doesn't seem to come naturally to everyone.
If you're not accustomed to writing operations, I think it really pays to
train yourself into that habit.
It's inconvenient to type a long message into the computer in the form of an
input to a procedure. Another approach would be a conversational front
end. This is a procedure that reads the cleartext message using
readlist, perhaps accepting the message over several lines. It's not hard
to write:
to encode.big.message local [keyword cleartext] print [Welcome to the Playfair enciphering program.] print [What keyword would you like to use?] make "keyword first readlist print [Now please enter your message, using as many lines as needed.] print [When you're done, enter a line containing only a period (.).] make "cleartext [] read.big.message print [Here is the enciphered version:] print [] print playfair :keyword :cleartext end to read.big.message local "line make "line readlist if equalp :line [.] [stop] make "cleartext sentence :cleartext :line read.big.message end
Such a top-level procedure may be justified in a project like this, in which a very large block of text may be used as a datum. But don't get carried away. Programming languages that don't emphasize composition of functions encourage this sort of programming style, to the point where the part of the program that prompts the user and reads the data gets to be longer than the part that does the actual computation. This preoccupation with verbose conversation between the program and the user is sometimes justified by the idea of "good human engineering," but I don't think that's necessarily true. To take an extreme case, consider the standard elementary school Logo procedure to draw a square:
to square :size repeat 4 [forward :size right 90] end
Compare that to this "human engineered" version:
to square local "size print [Brian's square program copyright 1985] print [What size square would you like me to draw?] make "size first readlist repeat 4 [forward :size right 90] print [Thank you, please come again.] end
Not only is the first version (in my opinion) much more pleasant
to use, but it is also more powerful and flexible. The second version can
be used only as a top-level program, carrying on a conversation with
a human user. The first version can be run at top level, but it can also be
used as a subprocedure of a more complicated drawing program. If it's used
at top level, some person types in a number, the size, as the input to
square on the instruction line. If it's used inside another procedure,
that procedure can compute the input.
I haven't described the part of the program that actually transforms
the message: the procedure encode and its subprocedures. Read
the listing at the end of the chapter, then answer these questions:
»Why does encode need two base cases?
»What purpose is served by the four invocations of thing at the
beginning of procedure paircode?
Of course this program can be improved in many ways.
»One straightforward improvement to this program would be to "bulletproof" it so that it doesn't die with a Logo error message if, for example, the user provides a bad keyword. (Instead, the program should give its own message, making it clear what the problem is. It's better for the user to see
Keywords may not have any letter repeated.
than
t has no value in paircode
after making that mistake.) Also, what if the cleartext input contains words with characters other than letters? The program should just ignore those characters and process the letters in the words correctly.
»Another fairly straightforward improvement would be to take the one
long word output by playfair and turn it into a list of words with
spacing and punctuation thrown in at random. The goal is to have the result
look more or less like an actual paragraph of English text, except for the
scrambled letters.
Another direction would be to work on deciphering a Playfair-coded message. There are two problems here: the easy one, in which you know what the keyword is, and the hard one, in which you know only that a Playfair cipher was used.
»The procedure playfair itself will almost work in
the first case. It would work perfectly were it not for the special cases
of letters in the same row and column. It's a simple modification to handle
those cases correctly. An interesting extension would be to try to restore
the original spacing by using a dictionary to guess where words end.
»The much harder problem is to try to guess the keyword. I mentioned earlier some ideas about the approaches you'd have to take, such as exploring the frequencies of use of pairs of letters. If you want more advice, you'll have to study books on cryptography.
| (back to Table of Contents) | BACK chapter thread NEXT |
to playfair :keyword :message
local [matrix a b c d e f g h i j k l m n o p q r s t u v w x y z]
setkeyword jtoi lowercase :keyword
output encode (reduce "word :message)
end
;; Prepare the code array
to setkeyword :word
make "matrix reorder word :word (remove :word "abcdefghiklmnopqrstuvwxyz)
make "j :i
end
to remove :letters :string
if emptyp :string [output "]
if memberp first :string :letters [output remove :letters bf :string]
output word first :string remove :letters bf :string
end
to reorder :string
output reorder1 :string (mdarray [5 5]) 1 1
end
to reorder1 :string :array :row :column
if :row=6 [output :array]
if :column=6 [output reorder1 :string :array :row+1 1]
mdsetitem (list :row :column) :array first :string
make first :string (list :row :column)
output reorder1 (butfirst :string) :array :row :column+1
end
;; Encode the message
to encode :message
if emptyp :message [output "]
if emptyp butfirst :message [output paircode first :message "q]
if equalp (jtoi first :message) (jtoi first butfirst :message) ~
[output word (paircode first :message "q) (encode butfirst :message)]
output word (paircode first :message first butfirst :message) ~
(encode butfirst butfirst :message)
end
to paircode :one :two
local [row1 column1 row2 column2]
make "row1 first thing :one
make "column1 last thing :one
make "row2 first thing :two
make "column2 last thing :two
if :row1 = :row2 ~
[output letters (list :row1 rotate (:column1+1)) ~
(list :row1 rotate (:column2+1))]
if :column1 = :column2 ~
[output letters (list rotate (:row1+1) :column1) ~
(list rotate (:row2+1) :column1)]
output letters (list :row1 :column2) (list :row2 :column1)
end
to rotate :index
output ifelse :index = 6 [1] [:index]
end
to letters :one :two
output word letter :one letter :two
end
to letter :rowcol
output itoj mditem :rowcol :matrix
end
;; I and J conversion
to jtoi :word
output map [ifelse equalp ? "j ["i] [?]] :word
end
to itoj :letter
if :letter = "i [if (random 3) = 0 [output "j]]
output :letter
end
Brian Harvey,
bh@cs.berkeley.edu