
| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |

|
|
When people first meet the idea of recursive procedures, they almost
always think there is some sort of magic involved. "How can that
possibly work? That procedure uses itself as a subprocedure! That's
not fair." To overcome that sense of unfairness, the combining method
works up to a recursive procedure by starting small, so that each step
is completely working before the next step, to solve a larger problem,
relies on it. There is no mystery about allowing downup5 to rely on
downup4.
The trouble with the combining method is that it's too much effort to be practical. Once you believe in recursion, you don't want to have to write a special procedure for a size-one problem, then another special procedure for a size-two problem, and so on; you want to write the general recursive solution right away. I'm calling this the "leap of faith" method because you write a procedure while taking on faith that you can invoke the same procedure to handle a smaller subproblem.
Let's look, once more, at the problem we were trying to solve when
writing the downup procedure. We wanted the program to behave
like this:
? downup "hello hello hell hel he h he hel hell hello
The secret of recursive programming is the same as a secret
of problem solving in general: see if you can reduce a big problem to
a smaller problem. In this case we can look at the printout from
downup this way:
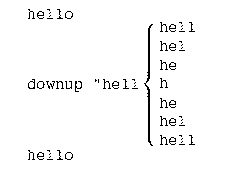
What I've done here is to notice that the printout from applying
downup to a five-letter word, hello, includes within itself the
printout that would result from applying downup to a smaller
word, hell.
This is where the leap of faith comes in. I'm going to pretend that
downup already works for the case of four-letter words.
We haven't begun to write the procedure yet, but never mind that. So
it seems that in order to evaluate the instruction
downup "hello
we must carry out these three instructions:
print "hello downup "hell print "hello
(The two print instructions print the first and last
lines of the desired result, the ones that aren't part of the smaller
downup printout.)
To turn these instructions into a general procedure, we must use a
variable in place of the specific word hello. We also have to
figure out the general relationship that is exemplified by the
transformation from hello into hell. This relationship
is, of course, simply butlast. Here is the procedure that
results from this process of generalization:
to downup :word print :word downup butlast :word print :word end
As you already know, this procedure won't quite work. It lacks a stop
rule. But once we have come this far, it's a relatively simple matter
to add the stop rule. All we have to do is ask ourselves, "What's
the smallest case we want the program to handle?" The answer is that
for a single-letter word the downup should just print the word
once. In other words, for a single-letter word, downup should
carry out its first instruction and then stop. So the stop rule goes
after that first instruction, and it stops if the input has only one
letter:
to downup :word print :word if equalp count :word 1 [stop] downup butlast :word print :word end
Voilà!
The trick is not to think about the stop rule at first. Just accept, on faith, that the procedure will somehow manage to work for inputs that are smaller than the one you're interested in. Most people find it hard to do that. Since you haven't written the program yet, after all, the faith I'm asking you to show is really unjustified. Nevertheless you have to pretend that someone has already written a version of the desired procedure that works for smaller inputs.
Let's take another example from Chapter 7.
? one.per.line "hello h e l l o
There are two different ways in which we can find a smaller pattern within this one. First we might notice this one:
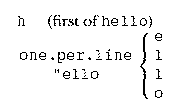
This pattern would lead to the following procedure, for which I haven't yet invented a stop rule.
to one.per.line :word print first :word one.per.line butfirst :word end
Alternatively we might notice this pattern:

In that case we'd have a different version of the procedure. This one, also, doesn't yet have a stop rule.
to one.per.line :word one.per.line butlast :word print last :word end
Either of these procedures can be made to work by adding the appropriate stop rule:
if emptyp :word [stop]
This instruction should be the first in either procedure.
Since both versions work, is there any reason to choose one over the
other? Well, there's no theoretical reason but there is a practical
one. It turns out that first and butfirst work faster
than last and butlast. It also turns out that procedures
that are tail recursive (that is, with the recursion step at the end)
can survive more levels of invocation, without running out of memory,
than those that are recursive in other ways. For both of
these reasons the first version of one.per.line is a better
choice than the second. (Try timing both versions with a very long
list as input.)
»Rewrite the say procedure
from Chapter 5 recursively.
If we think of
to one.per.line :word print first :word one.per.line butfirst :word end
merely as a statement of a true fact
about the "shape" of the result printed by
one.per.line, it's not very remarkable. The amazing part is that
this fragment is runnable!* It doesn't look runnable because it invokes itself as a
helper procedure, and--if you haven't already been through the combining
method--that looks as if it can't work. "How can you use one.per.line
when you haven't written it yet?"
*Well, almost. It needs a base
case.
The leap of faith method is the assumption that the procedure we're in the
middle of writing already works. That is, if we're thinking about writing a
one.per.line procedure that can compute one.per.line "hello, we
assume that one.per.line "ello will work.
Of course it's not really a leap of faith, in the sense of something
accepted as miraculous but not understood. The assumption is justified
by our understanding of the combining method. For example, we understand
that the five-letter one.per.line is relying on the four-letter version of
the problem, not really on itself, so there's no circular reasoning involved.
And we know that if we had to, we could write one.per.line1 through
one.per.line4 "by hand."
The reason that the technique in this chapter may seem more mysterious than
the combining method is that this time we are thinking about the problem
top-down. In the combining method, we had already written whatever4
before we even raised the question of whatever5. Now we start by
thinking about the larger problem and assume that we can rely on the
smaller one. Again, we're entitled to that assumption because we've gone
through the process from smaller to larger so many times already.
The leap of faith method, once you understand it, is faster than the combining method for writing new recursive procedures, because you can write the recursive solution immediately, without bothering with many individual cases. The reason I showed you the combining method first is that the leap of faith method seems too much like magic, or like "cheating," until you've seen several believable recursive programs. The combining method is the way to learn about recursion; the leap of faith method is the way to write recursive procedures once you've learned.
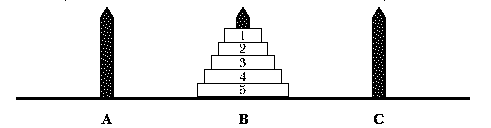
One of the most famous recursive problems is a puzzle called the Tower of Hanoi. You can find this puzzle in toy stores; look for a set of three posts and five or six disks. You start out with the puzzle arranged like this:

The object of the puzzle is to move all of the disks to the second post, like this:
This looks easy, but there are rules you must follow. You can only move one disk at a time, and you can't put a disk on top of a smaller disk. You might start trying to solve the puzzle this way:
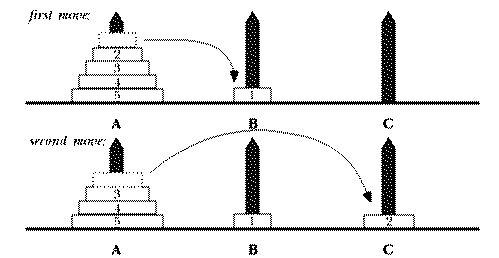
After that, you could move disk number 1 either onto post A, on top of disk 3, or onto post C, on top of disk 2.
I'm about to describe a solution to the puzzle, so if you want to work on it yourself first, stop reading now.
In the examples of downup and one.per.line, we identified
each problem as one for which a recursive program was appropriate
because within the pattern of the overall solution we found a smaller,
similar pattern. The same principle will apply in this case. We want
to end up with all five disks on post B. To do that, at some point we
have to move disk 5 from post A to post B. To do that, we first
have to get the other four disks out of the way. Specifically, "out
of the way" must mean onto post C. So the solution to the problem
can be represented graphically this way, in three parts:

The first part of the solution is to move disks 1 through 4 from post A to post C. The second part is a single step, moving disk 5 from post A to post B. The third part, like the first, involves several steps, to move disks 1 through 4 from post C to post B.
If you've developed the proper recursive spirit, you'll now say, "Aha! The first part and the third part are just like the entire puzzle, only with four disks instead of five!" I hope that after this example you'll develop a sort of instinct that will let you notice patterns like that instantly. You should then be ready to make a rough draft of a procedure to solve the puzzle:
to hanoi :number hanoi :number-1 movedisk :number hanoi :number-1 end
Of course, this isn't at all a finished program. For one thing, it
lacks a stop rule. (As usual, we leave that part for last.) For
another, we have to write the subprocedure movedisk that moves a
single disk. But a more important point is that we've only provided
for changing the disk number we're moving, not for selecting which
posts to move from and to. You might want to supply hanoi with
two more inputs, named from and to, which would be the
names of the posts. So to solve the puzzle we'd say
hanoi 5 "A "B
But that's not quite adequate. Hanoi also needs to
know the name of the third post. Why? Because in the
recursive calls, that third post becomes one of the two "active"
ones. For example, here are the three steps in solving the five-disk
puzzle:
hanoi 4 "A "C movedisk 5 "A "B hanoi 4 "C "B
You can see that both of the recursive invocations need to
use the name of the third post. Therefore, we'll give hanoi a
fourth input, called other, that will contain that name. Here
is another not-quite-finished version:
to hanoi :number :from :to :other hanoi :number-1 :from :other :to movedisk :number :from :to hanoi :number-1 :other :to :from end
This version still lacks a stop rule, and we still have to write
movedisk. But we're much closer. Notice that movedisk does
not need the name of the third post as an input. Its job is to
take a single step, moving a single disk. The unused post really has
nothing to do with it. Here's a simple version of movedisk:
to movedisk :number :from :to print (sentence [Move disk] :number "from :from "to :to) end
What about the stop rule in hanoi? The first thing that will
come to your mind, probably, is that the case of moving disk number 1
is special because there are no preconditions. (No other disk can
ever be on top of number 1, which is the smallest.) So you might want
to use this stop rule:
if equalp :number 1 [movedisk 1 :from :to stop]
Indeed, that will work. (Where would you put it in the procedure?) But it turns out that a slightly more elegant solution is possible. You can let the procedure for disk 1 go ahead and invoke itself recursively for disk number 0. Since there is no such disk, the procedure then has nothing to do. By this reasoning the stop rule should be this:
if equalp :number 0 [stop]
You may have to trace out the procedure to convince yourself
that this really works. Convincing yourself is worth the effort,
though; it turns out that very often you can get away with allowing
an "extra" level of recursive invocation that does nothing. When
that's possible, it makes for a very clean-looking procedure. (Once
again, I've left you on your own in deciding where to insert this stop
rule in hanoi.)
If your procedure is working correctly, you should get results like this for a small version of the puzzle:
? hanoi 3 "A "B "C Move disk 1 from A to B Move disk 2 from A to C Move disk 1 from B to C Move disk 3 from A to B Move disk 1 from C to A Move disk 2 from C to B Move disk 1 from A to B
If you like graphics programming and have been impatient to see a
turtle in this book, you might want to write a graphic version of
movedisk that would actually display the moves on the screen.
Suppose that, instead of downup, we wanted to write
updown, which works like this:
? updown "hello h he hel hell hello hell hel he h
It's harder to find a smaller subproblem within this pattern.
With downup, removing the first and last lines of the printout left a
downup pattern for a shorter word. But the middle lines of this
updown pattern aren't an updown. The middle lines don't start with a
single letter, like the h in the full pattern. Also, the middle lines
are clearly made out of the word hello, not some shortened version of
it. » You might want to try to find a solution yourself before
reading further.
There are several approaches to writing updown. One thing we
could do is to divide the pattern into two parts:
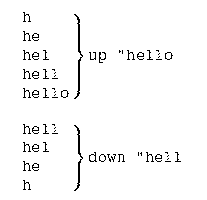
It is relatively easy to invent the procedures up and
down to create the two parts of the pattern.
to up :word if emptyp :word [stop] up butlast :word print :word end to down :word if emptyp :word [stop] print :word down butlast :word end
Then we can use these as subprocedures of the complete
updown:
to updown :word up :word down butlast :word end
Another approach would be to use numbers to keep track of things, as
in the inout example of Chapter 7. In this case we can
consider the middle lines as a smaller version of the problem.
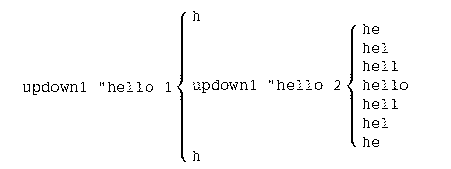
In this point of view all the inner, smaller updown patterns
are made from the same word, hello. But each invocation of
updown1 (which is what I'll call this version of updown)
will use a second input, a number that tells it how many
letters to print in the first and last lines:
? updown1 "hello 3 hel hell hello hell hel ? updown1 "hello 5 hello
We need a subprocedure, truncate, that prints the
beginning of a word, up to a certain number of letters.
to truncate :word :size if equalp count :word :size [print :word stop] truncate butlast :word :size end to updown1 :word :size truncate :word :size if equalp count :word :size [stop] updown1 :word :size+1 truncate :word :size end
(The helper procedure truncate is the sort of thing that
should really be an operation, for the same reason that second was
better than prsecond here.
We'll come back to the
writing of recursive operations in Chapter 11.)
Finally, we can write a new superprocedure called
updown that uses updown1 with the correct inputs. (If you try
all these approaches on the computer, remember that you can have only
one procedure named updown in your workspace at a time.)
to updown :word updown1 :word 1 end
A third approach, which illustrates a very powerful technique, also
uses an initialization procedure updown and a subprocedure
updown1 with two inputs. In this version, though, both inputs to the
subprocedure are words: the partial word that we're printing right
now and the partial word that is not yet to be printed.
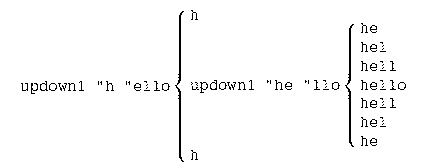
In this
example, to print an updown pattern for the word hello,
the two subprocedure inputs would be h (what's printed on the
first line) and ello (what isn't printed there). For the inner
pattern with the first and last lines removed, the two inputs would be
he and llo. Here is the program:
to updown1 :now :later print :now if emptyp :later [stop] updown1 (word :now first :later) butfirst :later print :now end to updown :word updown1 first :word butfirst :word end
This program may be a little tricky to understand. The
important part is updown1. Read it first without paying
attention to the stop rule; see if you can understand how it
corresponds to the updown pattern. A trace of its recursive invocations
might help:
updown "hello
updown1 "h "ello
updown1 "he "llo
updown1 "hel "lo
updown1 "hell "o
updown1 "hello "
The innermost level of recursion has been reached when the second
input is the empty word. Notice how first, butfirst, and
word are used in combination to calculate the inputs.
»Write a recursive procedure slant that takes a word as input and
prints it on a diagonal, one letter per line, like this:
? slant "salami
s
a
l
a
m
i
Just as Logo programs can be iterative or recursive, so can English sentences. People are pretty good at understanding even rather long iterative sentences: "This is the farmer who kept the cock that waked the priest that married the man that kissed the maiden that milked the cow that tossed the dog that worried the cat that killed the rat that ate the malt that lay in the house that Jack built." But even a short recursive (nested) sentence is confusing: "This is the rat the cat the dog worried killed."
»Write a procedure that takes as its first input a list of noun-verb pairs representing actor and action, and as its second input a word representing the object of the last action in the list. Your procedure will print two sentences describing the events, an iterative one and a nested one, following this pattern:
? scramble [[girl saw] [boy owned] [dog chased] [cat bit]] "rat This is the girl that saw the boy that owned the dog that chased the cat that bit the rat This is the rat the cat the dog the boy the girl saw owned chased bit
You don't have to worry about special cases like "that Jack built"; your sentences will follow this pattern exactly.
Ordinarily the most natural way to program this problem would be as an
operation that outputs the desired sentence, but right now we are
concentrating on recursive commands, so you'll write a procedure that
prints each line as shown above.
Certain patterns come up over and over in programming problems. It's
worth your while to learn to recognize some of them. For example,
let's look again at one.per.line:
to one.per.line :word if emptyp :word [stop] print first :word one.per.line butfirst :word end
This is an example of a very common pattern:
to procedure :input if emptyp :input [stop] do.something.to first :input procedure butfirst :input end
A procedure pattern is different from the result patterns we examined earlier in this chapter. Before we were looking at what we wanted a not-yet-written procedure to accomplish; now we are looking at already-written procedures to find patterns in their instructions. A particular procedure might look like this pattern with the blanks filled in. Here's an example:
to praise :flavors if emptyp :flavors [stop] print sentence [I love] first :flavors praise butfirst :flavors end ? praise [[ultra chocolate] [chocolate cinnamon raisin] ginger] I love ultra chocolate I love chocolate cinnamon raisin I love ginger
Do you see how praise fits the pattern?
»Continuing our investigation of literary forms, write a procedure to compose love poems, like this:
? lovepoem "Mary M is for marvelous, that's what you are. A is for awesome, the best by far. R is for rosy, just like your cheek. Y is for youthful, with zest at its peak. Put them together, they spell Mary, The greatest girl in the world.
The core of this project is a database of deathless lines, in the form of a list of lists:
make "lines [[A is for albatross, around my neck.]
[B is for baloney, your opinions are dreck.]
[C is for corpulent, ...] ...]
and a recursive procedure select that takes a letter and a
list of lines as inputs and finds the appropriate line to print by comparing
the letter to the beginning of each line in the list.
Another common pattern is a recursive procedure that counts something
numerically, like countdown:
to countdown :number if equalp :number 0 [stop] print :number countdown :number-1 end
And here is the pattern:
to procedure :number if equalp :number 0 [stop] do.something procedure :number-1 end
A procedure built on this pattern is likely to have additional inputs so that it can do something other than just manipulate the number itself. For example:
to manyprint :number :text if equalp :number 0 [stop] print :text manyprint :number-1 :text end ? manyprint 4 [Lots of echo in this cavern.] Lots of echo in this cavern. Lots of echo in this cavern. Lots of echo in this cavern. Lots of echo in this cavern. to multiply :letters :number if equalp :number 0 [stop] print :letters multiply (word :letters first :letters) :number-1 end ? multiply "f 5 f ff fff ffff fffff
One way to become a skillful programmer is to study other people's programs carefully. As you read the programs in this book and others, keep an eye open for examples of patterns that you think might come in handy later on.
Suppose that instead of one.per.line we'd like a procedure to print
the members of a list two per line. (This is plausible if we have a
list of many short items, for example. We'd probably want to control the
spacing on each line so that the items would form two columns, but let's not
worry about that yet.)
The recursive part of this program is fairly straightforward:
to two.per.line :stuff print list (first :stuff) (first butfirst :stuff) two.per.line butfirst butfirst :stuff end
The only thing out of the ordinary is that the recursive step uses a subproblem that's smaller by two members, instead of the usual one.
But it's easy to fall into a trap about the stop rule. It's not good enough to say
if emptyp :stuff [stop]
because in this procedure it matters whether the length of the input is odd or even. These two possibilities give rise to two stop rules. For an even-length list, we stop if the input is empty. But for an odd-length list, we must treat the case of a one-member list specially also.
to two.per.line :stuff if emptyp :stuff [stop] if emptyp butfirst :stuff [show first :stuff stop] print list (first :stuff) (first butfirst :stuff) two.per.line butfirst butfirst :stuff end
It's important to get the two stop rules in the right order; we
must be sure the input isn't empty before we try to take its butfirst.
»Why does this procedure include one show instruction and one
print instruction? Why aren't they either both show or both
print?
Brian Harvey,
bh@cs.berkeley.edu