
| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |

|
|
Program file for this chapter: crypto
A cryptogram is a kind of word puzzle, like a crossword puzzle. Instead of definitions, though, a cryptogram gives you the actual words of a quotation, but with each letter replaced with a different letter. For example, each letter A in the original text might be replaced with an F. Here is a sample cryptogram:
LB RA, BT YBL LB RA: LJGL CQ LJA FUAQLCBY: KJALJAT 'LCQ YBRXAT CY LJA DCYP LB QUSSAT LJA QXCYWQ GYP GTTBKQ BS BULTGWABUQ SBTLUYA, BT LB LGHA GTDQ GWGCYQL G QAG BS LTBURXAQ, GYP RM BIIBQCYW AYP LJAD?
The punctuation marks and the spaces between words are the same in this cryptogram as they are in the original ("clear") text.
A cryptogram is a kind of secret code. The formal name for this particular kind of code is a simple substitution cipher. Strictly speaking, a code is a method of disguising a message that uses a dictionary of arbitrarily chosen replacements for each possible word. A foreign language is like a code. A cipher is a method in which a uniform algorithm or formula is used to translate each word. A substitution cipher is one in which every letter (or sometimes every pair of letters, or some such grouping) is replaced by a disguised equivalent. A simple substitution cipher is one in which each letter has a single equivalent replacement, which is used throughout the message. (A more complicated substitution cipher might be something like this: the first letter A in the message is replaced with F, the second A is replaced with G, the third with H, and so on.)
Years ago, Arthur Conan Doyle and Edgar Allen Poe were able to write mystery stories in which simple substitution ciphers were used by characters who really wanted to keep a message secret. Today, partly because of those stories, too many people know how to "break" such ciphers for them to be of practical use. Instead, these ciphers are used as word puzzles.
The technique used for decoding a cryptogram depends on the fact that some letters are more common than others. The letter A is much more common in English words than the letter Z. If, in a cryptogram, the letter F occurs many times, it's more likely to represent a letter like A in the original text than a letter like Z.
The most commonly used letter in English is E, by a wide margin. T is in second place, with A and O nearly tied for third. I, N, and R are also very commonly used. These rankings apply to large texts. In the usual short cryptogram, the most frequent letter doesn't necessarily represent E. But the letter that represents E will probably be among the two or three most frequent.
Before reading further, you might want to try to solve the cryptogram shown above. Make a chart of the number of times each letter appears, then use that information to make guesses about which letter is which. As you're working on it, make a note of what other kinds of information are helpful to you.
This project is a program to help you solve cryptograms. The program doesn't solve the puzzle all by itself; it doesn't know enough about English vocabulary. But it does some of the more boring parts of the job automatically, and can make good guesses about some of the letters.
The top-level procedure is crypto . It takes one input, a list
whose members are the words of the cryptogram. Since these lists are long
and easy to make mistakes in, you'll probably find it easier to type the
cryptogram into the Logo editor rather than directly at a question mark
prompt. You might make the list be the value of a variable, then use that
variable as the input to crypto. (The program file for this
project includes four such variables, named cgram1 through
cgram4, with sample cryptograms.)
Crypto begins by going through the coded text, letter by letter.
It keeps count of how often each letter is used. You can keep track
of this counting process because the program draws a histogram
on the screen as it goes. A histogram is a chart like the one
at the top of the next page.
L B L AB L AB L AB L AB L AB L Q AB L Q Y AB G L Q T Y AB G L Q T Y AB G L Q T Y ABC G L Q T Y ABC G J L Q T Y ABC G J L Q TU Y ABC G J L QRSTU Y ABC G J L PQRSTU W Y ABCD G J L PQRSTU WXY ABCD G IJKL PQRSTU WXY ABCD FGHIJKLM PQRSTU WXY
Histogram
A-17-E B-18- C-08- D-03- E
F-01- G-11-A H-01- I-02- J-07-H
K-02- L-19-T M-01- N O
P-04- Q-13- R-05- S-05- T-11-
U-06- V W-04- X-03- Y-12-
Z
ABCDEFGHIJKLMNOPQRSTUVWXYZ
LB RA, BT YBL LB RA: LJGT CQ LJA
T E, T T E: THAT THE
FUAQLCBY: KJALJAT 'LCQ YBRXAT CY LJA
E T : HETHE 'T E THE
DCYP LB QUSSAT LJA QXCYWQ GYP GTTBKQ
T E THE A A
BS BULTGWABUQ SBTLUYA, BT LB LGHA
T A E T E, T TA E
GTDQ GWGCYQL G QAG BS LTBURXAQ, GYP
A A A T A EA T E , A
RM BIIBQCYW AYP LJAD?
E THE ?
Screen display
A histogram is a kind of graph, but it's different from the continuous graphs you use in algebra. Histograms are used to show quantities of discrete things, like letters of the alphabet.
The main reason the program draws the histogram is that it needs to know the frequencies of occurrence of the letters for later use. When I first wrote the program, it counted the letters without printing anything on the screen. Since this counting is a fairly slow process, it got boring waiting for the program to finish. The histogram display is a sort of video thumb-twiddling to keep you occupied while the program is creating an invisible histogram inside itself.
By the way, since there are only 24 lines on the screen, the top part of the histogram may be invisible if the cryptogram is long enough to use some letters more than 24 times.
The shape of this histogram is pretty typical. A few letters are used many times, while most letters are clumped down near the bottom. In this case, A, B, and L stand out. You might guess that they represent the most commonly used letters: E, T, and either A or O. But you need more information to be able to guess which is which.
After it finishes counting letters, the program presents a screen display like the one shown above. The information provided in this display comes in three parts. At the top is an alphabetical list of the letters in the cryptogram. For each letter, the program displays the number of times that letter occurs in the enciphered text. For example, the letter P occurs four times. The letter that occurs most frequently is highlighted by showing it in reverse video characters, represented here with underlined characters. In this example, the most frequently used letter is L, with 19 occurrences. Letters with occurrence counts within two of the maximum are also highlighted. In the example, A with 17 and B with 18 are highlighted. If a letter does not occur in the cryptogram at all, no count is given. In the example, there is no E in the enciphered text.
The top part of the display shows one more piece of information: if either the program or the person using it has made a guess as to the letter that a letter represents, that guess is shown after the frequency count. For example, here the program has guessed that the letter L in the cryptogram represents the letter T in the clear text. (You can't tell from the display that this guess was made by the program rather than by the person using it. I just happen to know that that's what happened in this example!)
The next section of the display is a single line showing all the letters of the alphabet. In this line, a letter is highlighted if a guess has been made linking some letter in the cryptogram with that letter in the clear text. In other words, this line shows the linkages in the reverse direction from what is shown in the top section of the display. For example, I just mentioned that L in the cryptogram corresponds to T in the clear text. In the top part of the display, we can find L in alphabetical order, and see that it has a T linked to it. But in the middle part of the display, we find T, not L, in alphabetical order, and discover that something is linked to it. (It turns out that we don't usually have to know which letter corresponds to T.)
Here is the purpose of that middle section of the display: Suppose I am looking at the second word of the cryptogram, RA. We've already guessed that A represents E, so this word represents something-E. Suppose I guess that this word is actually HE. This just happens to be the first two-letter word I think of that ends in E. So I'd like to try letting R represent H. Now I look in the middle section of the display, and I see that H is already highlighted. So some other letter, not R, already represents H. I have to try a different guess.
The most important part of the display is the bottom section. Here, lines of cryptogram alternate with their translation into clear text, based on the guesses we've made so far. The cryptogram lines are highlighted, just to make it easy to tell which lines are which. The program ensures that each word entirely fits on a single line; there is no wrapping to a new line within a single word.
There is room on the screen for eight pairs of lines. If the cryptogram is too big to fit in this space, only a portion of it will be visible at any time. In a few paragraphs I'll talk about moving to another section of the text.
The program itself is very limited in its ability to guess letters. For the most part, you have to do the guessing yourself when you use it. There are three guessing rules in the program:
In the example, the only single-letter word in the cryptogram is G, in the next-to-last line. The program, following rule 1, has guessed that G represents A. Rule 2 did not apply, because there is no second single-letter word. The most frequently used three-letter word is LJA, which occurs three times. The last letter of that word, A, is highlighted in the top section because it occurs 17 times. Therefore, the program guesses that L represents T, J represents H, and A represents E.
Of course you understand that these rules are not infallible; they're just guesses. (A fancy name for a rule that works most of the time is a heuristic. A rule that works all the time is called an algorithm.) For example, the three-letter word GYP appears twice in the cryptogram, only once less often than LJA. Maybe GYP is really THE. However, the appearance of the word THAT in the translation of the first line is a pretty persuasive confirmation that the program's rules have worked out correctly in this case.
If you didn't solve the cryptogram on your own, at my first invitation, you might want to take another look at it, based on the partial solution you now have available. Are these four letters (A, E, I, and T) enough to let you guess the rest? It's a quotation you'll probably recognize.
Once this display is on the screen, you can make further guesses by typing to the program. For example, suppose you decide that the last word of the cryptogram, LJAD, represents THEM. Then you want to guess that D represents M. To do that, type the letters D and M in that order. Don't use the RETURN key. Your typing will not be echoed on the screen. Instead, three things will happen. First, the entry in the top section of the display that originally said
D-03-
will be changed to say
D-03-M
Second, the letter M will be highlighted in the alphabet in the second section of the display. Finally, the program will type an M underneath every D in the cryptogram text.
If you change your mind about a guess, you can just enter a new guess about the same cryptogram letter. For example, if you decide that LJAD is really THEY instead of THEM, you could just type D and Y. Alternatively, if you decide a guess was wrong but you don't have a new guess, type the cryptogram letter (D in this example) and then the space bar.
If you guess that D represents M, and then later you guess that R also represents M, the program will complain at you by beeping or by flashing the screen, depending on what your computer can do. If you meant that R should represent M instead of D representing M, you must first undo the latter guess by typing D, space bar, R, and M.
The process of redisplaying the clear text translation of the cryptogram after each guess takes a fairly long time, since the program has to look up each letter individually. Therefore, the program is written so that you don't have to wait for this redisplay to finish before guessing another letter representation. As soon as you type any key on the keyboard, the program stops retyping the clear text. Whatever key you typed is taken as the first letter of a two-letter guess command.
If the cryptogram is too long to fit on the screen, there are three other things you can type to change which part of the text is visible. Typing a plus sign (+) eliminates the first four lines of the displayed text (that is, four lines of cryptogram and four corresponding lines of cleartext) and brings in four new lines at the end. Typing a minus sign (-) moves backwards, eliminating the four lines nearest the bottom of the screen and bringing back four earlier lines at the top. These windowing commands have no effect if you are already seeing the end of the text (for +) or the beginning of the text (for -).
The third command provided for long cryptograms is the atsign (@) character. This is most useful after you've figured out all of the letter correspondences. It clears the screen and displays only the clear text, without the letter frequencies, table of correspondences, or the enciphered text. This display allows 23 lines of clear text to fit on the screen instead of only eight. If you don't have the solution exactly right, you can type any character to return to the three-part display and continue guessing.
The program never stops; even after you have made guesses for all the letters, you might find an error and change your mind about a guess. When you're done, you stop the program with control-C or command-period or whatever your computer requires.
In the complete listing at the end of this chapter, there are a few cryptograms for you to practice with. They are excerpted from one of my favorite books, Compulsory Miseducation by Paul Goodman.
There are about 50 procedures in this program. These procedures can be roughly divided into several purposes:
The diagram on the next page shows superprocedure/subprocedure relationships within
the main categories. (Helper procedures aren't shown, to make the
diagram more readable.) The bottom half of the diagram has the
procedures that are concerned primarily with presenting information
on the screen. Redisplay, near the center of the diagram, is
called whenever the entire screen display must be redrawn: when the
initialization part of the program is finished, and whenever the user
chooses a new portion of the text to display. When the display
changes slightly, because a new guess is made, procedures such as
fixtop, light, and dark are used instead of redrawing
everything.
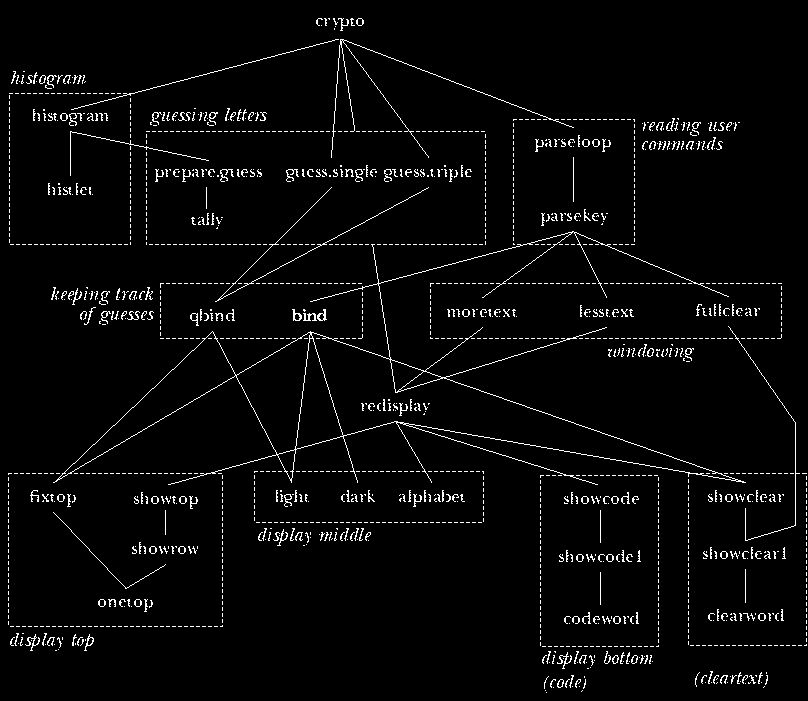
Bind is the most important procedure, because it records and displays
each new guess. As the diagram shows, it invokes several subprocedures to
update the display; more importantly, it changes the values of several
variables to keep track of the new guess. There is also a similar procedure
qbind that's used when a guess is made by the program rather than by
the user. (The "Q" stands for either "quick" or "quiet," since this
version never has to undo an old guess, omits some error checking, and can't
beep because there are no errors in automatic guesses.) If you ignore
initialization and displaying information, the entire structure of the
program is that crypto calls parseloop, which repeatedly calls
parsekey, which calls bind to record a guess.
Unfortunately, it's not so easy in practice to divide up the
procedures into groups, with a single purpose for each group. Several
procedures carry out two tasks at once. For example, light and
dark have those names because they switch individual letters
between normal and inverse video in the alphabet display in the middle
part of the screen. But those procedures also set variables to remember
that a particular cleartext letter has or hasn't been guessed, so they
are also carrying out part of bind's job, keeping track of guesses.
Crypto uses many global variables to hold the information it needs.
This includes information about individual letters, about
words, and about the text as a whole.
There are several sets of 26 variables, one for each letter of the alphabet. For these variables, the last letter of the variable name is the letter about which the variable holds information. In the table that follows, the italic x in each name represents any letter.
| x | Cleartext letter that is guessed to match x in the cryptogram. | |
|---|---|---|
boundx | True if x appears in the
cleartext as guessed so far; false otherwise.
| |
cntx | Count of how many times x appears in the cryptogram. | |
posnx | Screen cursor position where the frequency count and guess for x is shown in the top part of the display. |
These variables are set up initially by initvars, except
for the posn variables, which are set by showrow. The
variables with single-letter names start out with a space character as their
value. This choice allows showclear to use thing :letter
as the thing to type for every letter in the cryptogram.
If no guess has been made for a letter, it will be displayed as a
blank space in the partially-decoded version of the text.
Here are the variables that have to do with words in the cryptogram text. These variables are needed for the part of the program that automatically makes guesses, by looking for words that might represent A, I, and THE in the cleartext. In the following variable names, y represents either a one-letter word or a three-letter word in the cryptogram text.
count.single
| The number of occurrences of the most frequent one-letter word. | |
|---|---|---|
count.triple
| The number of occurrences of the most frequent three-letter word. | |
list.single
| List of one-letter words in the cryptogram text. | |
list.triple
| List of three-letter words in the cryptogram text. | |
max.single
| The most frequent one-letter word in the cryptogram text. | |
max.triple
| The most frequent three-letter word in the cryptogram text. | |
singley
| The number of occurrences of the one-letter word y. | |
tripley
| The number of occurrences of the three-letter word y. |
These variables are used only during the initial histogram counting, to keep track of which one-letter word and which three-letter word are the most frequent in each category. Once the most frequently occurring words have been determined, the actual count is no longer important.
Finally, there are some variables that contain information about the text as a whole:
fulltext
| The complete cryptogram text. | |
|---|---|---|
text
| The part of the cryptogram that is displayed on the screen right now. | |
moretext
| The part of the text that should be displayed
after a + command.
| |
textstack
| A list of old values of text, to be restored
if the - command is used.
| |
maxcount
| The number of occurrences of the most frequently used letter. |
:Maxcount is used to know which letters should be highlighted
in the top section of the display. :Text is used by showcode and
showclear to maintain the bottom section of the display.
Fulltext, moretext, and textstack are part of the windowing
feature. At first, text is equal to fulltext, and
textstack is empty. Moretext contains the portion of the text
starting on the fifth line that is displayed, providing there is some text
at the end of the cryptogram that didn't fit on the screen. If the end of
the text is visible, then moretext is empty. Here is what happens if
you type the plus sign:
to moretext if emptyp :moretext [beep stop] push "textstack :text make "text :moretext redisplay "true end
If :moretext is empty, there is no more text to display,
and the procedure stops with a complaint. Otherwise, we want
to remember what is now in :text in case of a later - command, and
we want to change the value of text to the version starting four lines
later that is already in :moretext.
In the solitaire project, I used a lot of local instructions in the
top-level procedures to avoid creating global variables. In this project,
I didn't bother. There's no good reason why I was lazier here than there;
you can decide for yourself whether you think it's worth the effort.
In revising this program for the second edition, I was struck by the ways in which bad choices of procedure or variable names had made it needlessly hard to read. Changing names was one of the three main ways in which I changed the program. (The other two were an increased use of data abstraction and the introduction of iteration tools to eliminate some helper procedures.)
I'll start with a simple example. As I've mentioned, when I first wrote
the program it didn't draw the histogram on the screen during the initial
counting of letter frequencies. Since the top part of the screen display
is primarily a presentation of those frequencies, I thought of that top
part as the program's "histogram" even though it doesn't have the form
of a real histogram. That's why, in the first edition, the procedures
that maintain the top part of the display were called showhist,
fixhist, and so on; when I added the histogram and histlet
procedures that draw the real histogram, it was hard to keep track of
which "hist" names were part of the initial histogram and which
were part of the letter frequency chart at the top of the program's normal
screen display. I've now changed showhist to showtop,
fixhist to fixtop, and so on. The procedures with hist
in their names are about the real histogram, and the ones with top
in their names are about the frequency chart.
Here's another example. In several parts of the program, I had to determine whether a character found in the cryptogram text is a letter or a punctuation mark. The most straightforward way to do this would be an explicit check against all the letters in the alphabet:
to letterp :char output memberp :char "ABCDEFGHIJKLMNOPQRSTUVWXYZ end
But comparing the character against each of the 26 letters
would be quite slow. Instead, I took advantage of the fact that there
happen to be variables in the program named after each letter. That is,
there's a variable A, a variable B, and so on, but there
aren't variables named after punctuation characters. Therefore, I could use
the Logo primitive namep to see whether or not the character I'm
considering is a variable name, and if so, it must be a letter. The
first edition version of crypto is full of instructions
of the form
if namep :char ...
This is clever and efficient, but not at all self-documenting.
Someone reading the program would have no way to tell that I'm using
namep to find out whether a character is a letter. The solution
was to add an instruction to the initialization in crypto:
copydef "letterp "namep
The copydef primitive is used to give a new name to
an existing procedure. (The old name continues to work.) The existing
procedure can be either primitive or user-defined. The new name is not
saved by the save command; that's why crypto performs the
copydef instruction each time.
Probably the worst example of bad naming was in the tally procedure.
This procedure has a complicated job; it must keep track of the most
common one-letter and three-letter words, in preparation for the program's
attempts to make automatic guesses for A, I, and THE. Here is the version
in the first edition:
to tally :type :word local "this make "this word :type :word if not memberp :word list. :type ~ [setlist. :type fput :word list. :type make :this 0] make :this sum 1 thing :this make "this thing :this if :this > (count. :type) ~ [setcount. :type :this make (word "max. :type) :word] end
The input named type is either the word single or
the word triple. One thing that makes this procedure hard to read
is the local variable named this. What a vague name! This what?
Is it this word, or this letter, or this word length, or this guess? To
make things worse, partway through the procedure I recycled the same
name to hold a different value. At first, :this is a word that
will be used as the name of a variable, counting the number of times
a given word appears. For example, if the word YBL appears in the
cryptogram, then tally will create a variable named tripleybl
whose value will be the number of times that YBL occurs in the text.
The value of this will be the word tripleybl, so the
expression thing :this represents the actual number. Then,
near the end of the procedure, I used the instruction
make "this thing :this
From then on, :this is the number itself, not the
variable name! It's really hard to read a procedure in which the
same name is used to mean different things in different instructions.
Here's the new version:
to tally :type :word localmake "countvar word :type :word if not memberp :word list. :type ~ [setlist. :type fput :word list. :type make :countvar 0] localmake "count (thing :countvar)+1 make :countvar :count if :count > (count. :type) ~ [setcount. :type :count setmax. :type :word] end
The name this is gone. Instead, I've first created
a local variable named countvar whose value is the name of the
count variable. Then I create another local variable named count
that contains the actual count. These names are much more descriptive
of the purposes of the two variables.
Another change in the new version is a more consistent use of
data abstraction. The original version used the constructor
setlist. and the selector list. to refer to the
list of all known cryptogram words of the appropriate length (the
variable list.single or list.triple), but
used the instruction
make (word "max. :type) :word
to construct the variable containing the most frequently
appearing word of that length. The new version uses a constructor
named setmax. that's analogous to the setlist. constructor.
Rethinking the names of procedures can reorganize your ideas about how
to group the procedures into categories. For example, in the first
edition I was upset about the fact that historgram, whose job
is to count letter frequencies and draw the histogram of those counts,
also invokes prepare.guess, whose job is to count word frequencies
in preparation for automatic guessing.
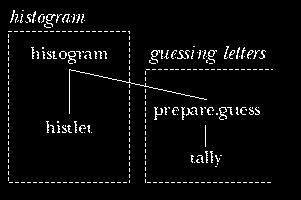
The reason for this mixture of tasks is efficiency. To prepare the histogram, the program must extract the letters (omitting punctuation) from each word of the text, and count them. To prepare for guessing words, the program must extract the letters from each word, and count the occurrences of the letters-only words. I could have done these things separately:
to histogram :text foreach :text [foreach (filter "letterp ?) "histlet] end to count.words :text foreach :text [prepare.guess (filter "letterp ?)] end
But it seemed better to scan the words of the text just once, and extract the letters from each word just once:
to histogram :text
foreach :text [localmake "word filter "letterp ?
foreach :word "histlet
prepare.guess :word]
end
But the punch line of this story is that I could avoid the
confusing jump between boxes--the feeling of mixing two tasks--merely
by changing the name of the histogram procedure to something
neutral like preprocess. Then the structure would be
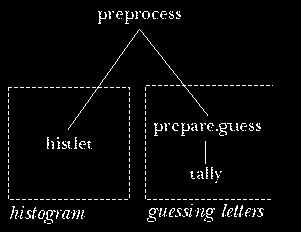
Now we have one initialization procedure that includes invocations
for two separate kinds of preprocessing. It's not
really the program structure that is inappropriate, but only using the
name histogram for a procedure whose job includes more than the
creation of the histogram.
Procedure redisplay has the job of redrawing the entire screen when
there is a major change to what should be shown, like moving to a different
window in the cryptogram text.
to redisplay :flag cleartext showtop alphabet showcode :text if :flag [showclear :text] end
The input to redisplay is a flag variable. It must
have the value true or false. (The name comes from the flags on
mailboxes, which are either up or down to indicate whether or not there is
mail in the box.) It's there because redisplay
has two slightly different
jobs to do at two different points in the program. First, redisplay
is invoked by crypto, the top-level procedure, to draw the screen
initially. At this time, no letters have been guessed yet. Therefore, it
is not necessary to invoke showclear (which indicates
the guessed letters in the bottom part of the display).
Crypto executes the instruction
redisplay "false
to avoid that unnecessary work. Redisplay is also invoked
by moretext, lesstext, and showclear. Each of these
procedures uses the instruction
redisplay "true
to include showcode. If the flag variable
weren't used, there would have to be two different versions
of redisplay.
I used the latter technique in the procedures bind and
qbind. These could also have been one procedure with a flag variable
input. The advantage of the technique used in redisplay is that it
makes the program easier to read by reducing the number of procedures, and
keeping similar purposes together. The advantage of using two procedures is
that it's a little faster, because you don't have to test the flag variable
with if.
A flag variable is somewhat analogous to a predicate, a
procedure that always outputs true or false. The
advantage of using these particular values for flag variables is that
they're easy to test; you can say
if :flag [do.something]
whereas, if you used some other pair of values like yes and
no, you'd have to say
if equalp :flag "yes [do.something]
Some people like to give flag variables names ending with p,
as in the convention for predicates. (The special variable redefp
that controls redefinition of primitives in some versions of Logo,
including Berkeley Logo, is an
example.) I'm somewhat uncomfortable with that practice because to me it
raises a confusion about whether a particular word is the name of a variable
or the name of a procedure. I'd rather put flag in the names of flag
variables.
The 26 boundx variables in this program are also flag
variables; each is true if the corresponding letter has been
guessed as the cleartext half of a binding. They don't have "flag"
in their names, but their names aren't used directly in most of the
program anyway. Instead they are hidden behind data abstraction procedures.
Setbound and setunbound are used to set any such variable
true or false, respectively; the selector boundp alerts
you by the P in its name that it's a predicate.
One of the ways in which I simplified the program for this edition was
to replace some recursive helper procedures with invocations of
foreach. At several points in the program, some action must be taken
for each letter in a word, or for each word in the text.
Another kind of iteration problem that was not so easily solved by
the standard higher order procedures in Berkeley Logo was one in which
some action must be taken, not for each letter in a word, but for
each letter in the alphabet, or for some subset of the alphabet, as
in the case of showrow, which displays one row of the top part
of the screen, with information about five consecutive letters.
Of course these problems could be solved with instructions like
foreach "ABCDEFGHIJKLMNOPQRSTUVWXYZ [...]
but that seemed unaesthetic to me. I wanted to be able to specify the starting and ending letters, as in this example:
to alphabet setcursor [6 6] forletters "A "Z [ifelse boundp ? [invtype ?] [type ?]] end
(The job of alphabet is to generate the middle
part of the screen display, which is all of the letters of the
alphabet, in order, with each letter in inverse video if that
letter has been guessed as part of the cleartext.)
The difficulty in implementing forletters is to get from one
letter to the next. How does a program know that the letter after
A is B? Here is my solution:
to forletters :from :to :action
for [lettercode [ascii :from] [ascii :to]] ~
[apply :action (list char :lettercode)]
end
The operation ascii
takes a letter (or other character)
as input. Its output is the number that represents that letter in
the computer's memory. Most computers use the same numbers to represent
characters; this standard representation is called ASCII, for
American Standard Code for Information Interchange. (It's
pronounced "ask E.") By using ascii to translate the starting
and ending letters into numeric codes, I've transformed the problem
into one that can be solved using the standard for tool that
allows an action to be carried out for each number in a given range.
But in the template input to forletters, I want the question mark
to represent a letter, not its numeric code.
Char is the inverse operation to ascii. Given
a number that is part
of the ASCII sequence, char outputs the character that that number
represents. For example:
?print ascii "A 65 ?print char 65 A
Forletters applies the template input to the character
corresponding to the number in the lettercode variable controlled by
the for.
Adding 1 to an ASCII code to get the code for the next letter depends on the fact that the numbers representing the letters are in sequence. Fortunately, this is true of ASCII. A is 65, B is 66, C is 67, and so on. Not all computer representations for characters have this property. The code that was used in the days of punched cards had the slash (/) character in between R and S!
By the way, the lower case letters have different ASCII codes from the
capitals. In this program I've used the primitive operation
uppercase to translate every character that the program reads
into upper case, just to be sure that each letter has only one
representation.
Another programming technique that is heavily used in this project
is the use of word to compute variable names dynamically. Ordinarily,
you assign a value to a variable named var with an instruction like
make "var 87
and you look at the value of the variable with the expression
:var
But in this project, there are variables for each letter,
with names like posna, posnb, posnc,
and so on. To assign a value to
these variables, the program doesn't use 26 separate instructions
like
make "posna [0 0]
(Each of these variables contains a list of screen coordinates for
use with setcursor to find the corresponding letter in the top part of
the display.) Instead, the procedure showrow, which draws that
section of the display, contains the instruction
forletters :from :to [setposn ? cursor onetop ?]
Setposn is a data abstraction procedure:
to setposn :letter :thing make (word "posn :letter) :thing end
When the variable letter contains the letter a,
the make instruction
has the same effect as if it were
make "posna :thing
Similarly, the dots notation (:posna) isn't used to examine the values
of these variables. Instead, thing is invoked explicitly:
to posn :letter output thing (word "posn :letter) end
Another point to consider is that I could have used a different approach
altogether, instead of using word to piece together a variable name.
For instance, I could have used property lists:
to setposn :letter :thing pprop "posn :letter :thing end to posn :letter output gprop "posn :letter end
As it happens, I first wrote this project in Atari 800 Logo, which
didn't have property list primitives. So the question didn't arise for
me. In a version of Logo that does support property lists, I see no
stylistic reason to prefer one approach over the other. It's
entirely a question of which is more efficient. Which is faster, searching
through a list of 26 times 2 members (times 2 because each property has a
name and a value) or concatenating strings with word to generate the
name of a variable that can then be examined quickly? I'd have to
experiment to find out. Alternatively, instead of using posn as the
name of a property list and the letters as names of properties, I could
reverse the two roles. That would give me more lists, but shorter lists.
What is a stylistic issue is that using procedures like posn
and setposn to isolate the storage mechanism from the rest of the
program makes the latter easier to read.
I have three suggestions about how to extend this project. The first is to put in more rules by which the program can make guesses automatically. For example, a three-letter word that isn't THE might be AND. Sequences of letters within a word can also be tallied; TH is a common two-letter sequence, for example. A double letter in the cryptogram is more likely to represent OO than HH.
If you have many rules in the program, there will be situations in
which two rules lead to contradictory guesses. One solution is just
to try the most reliable rule first, and ignore a new guess if it
conflicts with an old one. (Qbind applies this strategy by means
of the instruction
if letterp thing :from [stop]
which avoids adding a guess to the data base if the cryptogram letter is already bound to a cleartext letter.)
Another solution would be to let the rules "vote" about guesses. If the program had many rules, it might happen that three rules suggest that F represents E, while two rules suggest that W represents E. In this case, three rules outvote two rules, and the program would guess that F represents E.
The second direction for exploration in this program is to try to
make it more efficient. For example, every time you make a guess,
showclear is invoked to redisplay the partially decoded text. Much
of this redisplay is unnecessary, since most of the guesses haven't
changed. How can you avoid the necessity to examine every letter
of the cryptogram text? One possibility would be to keep a list,
for every letter in the text, of the screen positions in which that
letter appears. Then when a new guess is made, the program could
just type the corresponding cleartext letter at exactly those positions.
The cost of this technique would be a lot of storage space for the
lists of positions, plus a slower version of showcode, which would
have to create these position lists.
The third direction for further exploration is to find out about more complicated ciphers. For example, suppose you started with a simple substitution cipher, but every time the letter A appeared in the cleartext you shifted the corresponding cryptogram letters by one. That is, if E is initially represented by R, the first time an A appears you'd start using S to represent E. The second time A appears you'd switch to T representing E. And so on. The effect of this technique would be that a particular cleartext letter is no longer represented by a single cryptogram letter all the way through. Therefore, you can't just count the frequencies of the cryptogram letters and assume that frequently-used letters represent E and T. How could you possibly decipher such a message?
| (back to Table of Contents) | BACK chapter thread NEXT |
to crypto :text
make "text map "uppercase :text
make "fulltext :text
make "moretext []
make "textstack []
if not procedurep "letterp [copydef "letterp "namep]
forletters "A "Z "initvars
make "maxcount 0
initcount "single
initcount "triple
cleartext
histogram :text
redisplay "false
if or guess.single guess.triple [showclear :text]
parseloop
end
;; Initialization
to initcount :type
setlist. :type []
setcount. :type 0
end
to initvars :letter
setcnt :letter 0
make :letter "| |
setunbound :letter
end
;; Histogram
to histogram :text
foreach :text [localmake "word filter "letterp ?
foreach :word "histlet
prepare.guess :word]
end
to histlet :letter
localmake "cnt 1+cnt :letter
setcursor list (index :letter) (nonneg 24-:cnt)
type :letter
setcnt :letter :cnt
if :maxcount < :cnt [make "maxcount :cnt]
end
;; Guessing letters
to prepare.guess :word
if equalp count :word 1 [tally "single :word]
if equalp count :word 3 [tally "triple :word]
end
to tally :type :word
localmake "countvar word :type :word
if not memberp :word list. :type ~
[setlist. :type fput :word list. :type make :countvar 0]
localmake "count (thing :countvar)+1
make :countvar :count
if :count > (count. :type) ~
[setcount. :type :count setmax. :type :word]
end
to guess.single
if emptyp (list. "single) [output "false]
if emptyp butfirst (list. "single) ~
[qbind first (list. "single) "A output "true]
qbind (max. "single) "A
qbind (ifelse equalp first (list. "single) (max. "single)
[last (list. "single)]
[first (list. "single)]) ~
"I
output "true
end
to guess.triple
if emptyp (list. "triple) [output "false]
if :maxcount < (3+cnt last (max. "triple)) ~
[qbind first (max. "triple) "T
qbind first butfirst (max. "triple) "H
qbind last (max. "triple) "E
output "true]
output "false
end
;; Keyboard commands
to parseloop
forever [parsekey uppercase readchar]
end
to parsekey :char
if :char = "@ [fullclear stop]
if :char = "+ [moretext stop]
if :char = "- [lesstext stop]
if not letterp :char [beep stop]
bind :char uppercase readchar
end
;; Keeping track of guesses
to bind :from :to
if not equalp :to "| | [if not letterp :to [beep stop]
if boundp :to [beep stop]]
if letterp thing :from [dark thing :from]
make :from :to
fixtop :from
if letterp :to [light :to]
showclear :text
end
to qbind :from :to
if letterp thing :from [stop]
make :from :to
fixtop :from
light :to
end
;; Maintaining the display
to redisplay :flag
cleartext
showtop
alphabet
showcode :text
if :flag [showclear :text]
end
;; Top section of display (letter counts and guesses)
to showtop
setcursor [0 0]
showrow "A "E
showrow "F "J
showrow "K "O
showrow "P "T
showrow "U "Y
showrow "Z "Z
end
to showrow :from :to
forletters :from :to [setposn ? cursor onetop ?]
print []
end
to onetop :letter
localmake "count cnt :letter
if :count = 0 [type word :letter "| | stop]
localmake "text (word :letter "- twocol :count "- thing :letter)
ifelse :maxcount < :count+3 [invtype :text] [type :text]
type "| |
end
to twocol :number
if :number > 9 [output :number]
output word 0 :number
end
to fixtop :letter
setcursor posn :letter
onetop :letter
end
;; Middle section of display (guessed cleartext letters)
to alphabet
setcursor [6 6]
forletters "A "Z [ifelse boundp ? [invtype ?] [type ?]]
end
to light :letter
setcursor list 6+(index :letter) 6
invtype :letter
setbound :letter
end
to dark :letter
setcursor list 6+(index :letter) 6
type :letter
setunbound :letter
end
;; Bottom section of display (coded text)
to showcode :text
make "moretext []
showcode1 8 0 :text
end
to showcode1 :row :col :text
if emptyp :text [make "moretext [] stop]
if :row > 22 [stop]
if and equalp :row 16 equalp :col 0 [make "moretext :text]
if (:col+count first :text) > 37 [showcode1 :row+2 0 :text stop]
codeword :row :col first :text
showcode1 :row (:col+1+count first :text) butfirst :text
end
to codeword :row :col :word
setcursor list :col :row
invtype :word
end
;; Bottom section of display (cleartext)
to showclear :text
showclear1 8 0 :text 2
end
to showclear1 :row :col :text :delta
if emptyp :text [stop]
if :row > 23 [stop]
if keyp [stop]
if (:col+count first :text) > 37 ~
[showclear1 :row+:delta 0 :text :delta stop]
clearword :row :col first :text
showclear1 :row (:col+1+count first :text) butfirst :text :delta
end
to clearword :row :col :word
setcursor list :col :row+1
foreach :word [ifelse letterp ? [type thing ?] [type ?]]
end
;; Windowing commands
to fullclear
cleartext
showclear1 0 0 :fulltext 1
print []
invtype [type any char to redisplay]
ignore readchar
redisplay "true
end
to moretext
if emptyp :moretext [beep stop]
push "textstack :text
make "text :moretext
redisplay "true
end
to lesstext
if emptyp :textstack [beep stop]
make "text pop "textstack
redisplay "true
end
;; Iteration tool for letters
to forletters :from :to :action
for [lettercode [ascii :from] [ascii :to]] ~
[apply :action (list char :lettercode)]
end
;; Data abstraction (constructors and selectors)
to setbound :letter
make word "bound :letter "true
end
to setunbound :letter
make word "bound :letter "false
end
to boundp :letter
output thing word "bound :letter
end
to setcnt :letter :thing
make (word "cnt :letter) :thing
end
to cnt :letter
output thing (word "cnt :letter)
end
to setposn :letter :thing
make (word "posn :letter) :thing
end
to posn :letter
output thing (word "posn :letter)
end
to setcount. :word :thing
make (word "count. :word) :thing
end
to count. :word
output thing (word "count. :word)
end
to setlist. :word :thing
make (word "list. :word) :thing
end
to list. :word
output thing (word "list. :word)
end
to setmax. :word :thing
make (word "max. :word) :thing
end
to max. :word
output thing (word "max. :word)
end
;; Miscellaneous helpers
to index :letter
output (ascii :letter)-(ascii "A)
end
to beep
tone 440 15
end
to invtype :text
type standout :text
end
to nonneg :number
output ifelse :number < 0 [0] [:number]
end
;; Sample cryptograms
make "cgram1 [Dzynufqyjulli, jpqhq ok yr hoxpj qnzeujory qceqwj xhrtoyx
zw oyjr u trhjptpolq trhln. oynqqn, rzh qceqkkogq eryeqhy tojp
whrvlqfk rd qnzeujory uj whqkqyj kofwli fquyk jpuj jpq |xhrty-zwk| nr
yrj pugq kzep u trhln. u nqeqyj qnzeujory uofk uj, whqwuhqk drh, u
frhq trhjptpolq dzjzhq, tojp u noddqhqyj erffzyoji kwohoj, noddqhqyj
reezwujoryk, uyn frhq hqul zjoloji jpuy ujjuoyoyx kjujzk uyn kuluhi.]
make "cgram2 [Lvo vfkp lfzj md opaxflimn iz lm gitokflo fnp zlkonblvon f
hmalv'z inilifliuo, fnp fl lvo zfyo liyo lm zoo lm il lvfl vo jnmwz
wvfl iz noxozzfkh lm xmco wilv lvo mnbminb fxliuilioz fnp xaglako md
zmxiolh, zm lvfl viz inilifliuo xfn to kogoufnl. il iz ftzakp lm
lvinj lvfl lviz lfzj xfn to fxxmycgizvop th zm yaxv zillinb in f tms
dfxinb dkmnl, yfnicagflinb zhytmgz fl lvo pikoxlimn md pizlfnl
fpyinizlkflmkz. lviz iz kflvok f wfh lm kobiyonl fnp tkfinwfzv.]
make "cgram3 [Pcodl hbdcx qxdrdlh yihcodr, hbd rzbiier gxd lih ziyqdhdlh
hi hdgzb gwhbdlhcz echdxgzf, xdgnclp gr g ydglr ia ecudxghcil gln
zwehcoghcil. gln c niwuh hbgh yirh ia wr jbi rdxciwref xdgn gln jxchd
hbd dlpecrb eglpwgpd dodx edgxldn ch uf hbd xiwhd ia "xwl, rqih, xwl"
hi rcegr ygxldx.]
make "cgram4 [Jw btn xnsgsyp ejke gfebbcg, dtyjbn fbccsksg, ryu fbccsksg
nswcsfpsu pes usgjns, wnssuba, ryu wtptns bw pes qbtyk, pesns zbtcu
ls yb knrujyk, yb psgpjyk svfsxp rg r psrfejyk aspebu, ryu yb
lcrfilbrnu dtykcsg. jy wrfp, zs rns ksppjyk cbfigpsx gfesutcjyk ryu
knrujyk pb pes xbjyp bw pbnptns.]
Brian Harvey,
bh@cs.berkeley.edu