
| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |

|
|
Program file for this chapter: solitaire
This program deals out a hand of solitaire and maintains a picture of the card layout as you play the game by entering commands to move cards. It doesn't try to provide help with strategy, but it does know the rules for legal moves.
This chapter follows Chapter 3 because the solitaire program uses
catch and throw for three kinds of nonlocal exit.
The program is an infinite loop that plays games repeatedly, so there is an
exit command that is implemented as a throw. Each game is
itself an infinite loop, processing user commands repeatedly until either
the game is won or the user asks to start a new game. The command to start
a new game is also implemented as a throw. Finally, if the
program detects an error in a user command, such as asking to move a card
that isn't playable, the program rings a bell and throws back
to the command-reading loop.
to solitaire ...initialization... catch "exit [forever [onegame]] end to onegame ...initialization... catch "endgame [forever [catch "bell [parsecmd]]] end
But what I actually find most interesting about this program is the way in which it interacts with the user. By now, most people have seen computer solitaire programs in which the cards are drawn graphically on the screen, and the user moves cards by dragging with a mouse. (A program of that kind is included with Microsoft Windows, and versions are also available for most other computer systems.) The advantage of the mouse interface is that it's very easy to learn. Once you've seen how dragging an object with the mouse works in a painting program or a word processor, it's immediately obvious how to drag cards in the solitaire program, without reading an instruction manual.
This Logo solitaire program doesn't use a mouse. Instead, you move cards with keyboard commands. Most of the time it takes a single keystroke to tell the program which card to move, and where to move it. The trouble is that you have to learn the command keys! Given the choice, I think that most people would rather start playing right away with a mouse-driven program than take the time to learn to use mine. But I actually find the Logo program easier to use. Typing a single key is faster and easier on the wrist than moving the mouse to where the card is, holding down the mouse button, moving the mouse to where you want to put the card, and then releasing the button.
There's no question that mouse-based graphical user interfaces have vastly increased the acceptance and use of computers by people who are not technical experts. And I was happy to have a mouse-based drawing program to produce many of the illustrations in these books! But I did the word processing with a keyboard-controlled text editor; I find it easier to use and more flexible than the mouse-based word processors. Maybe it's just incipient old age, but I'm still a holdout against the idea that everything is better done with a mouse.
Play several games using this program, and several using a mouse-based solitaire program, and see what you think.
Here is a picture of a solitaire game in progress.

In the center of the picture are seven stacks of cards. Each stack may include some hidden cards and some shown cards. The hidden cards, if any, are beneath the shown cards. If there are any cards at all in a stack, at least one must be shown. Cards that are not part of this layout are held in the hand and dealt from the hand onto the pile; the cards in the hand are hidden, while the top card of the pile is visible. At the top of the picture are four more piles of cards, one for each suit; I'll call these piles "the top" so that I can reserve the name pile for the one at the bottom.
Here is how the same layout would be represented by the program:
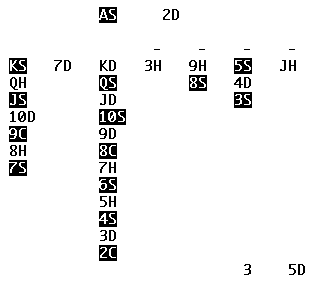
Shown cards are represented on the screen by the rank and suit of the card. Several cards may be shown in each stack, while only one card is shown in the pile, and one of each suit in the top. Each stack has a dash at the top of its display if there are any hidden cards in that stack; the hand is represented by the number of cards in it.
In playing solitaire it's important to distinguish black cards from red
cards, so the program does its best to present the color information to
you. The facilities for color display vary tremendously between computer
models, both in what capabilities are available and in the means by which
a program can use them. Berkeley Logo sacrifices versatility for
uniformity; there is a standout primitive operation that can
be used to print text in "reverse video," whichever of black-on-white
and white-on-black isn't the usual presentation.

The solitaire program displays red cards in normal text
and black cards in reverse video. The DOS version normally displays white
text on a black background, while the Macintosh version normally displays
black text on a white background, so the effect looks different on each
kind of computer.
There are many variations in the rules of solitaire, so I should describe in detail the version this program knows. In the initial layout, there are seven stacks. The first stack (on the left) has one shown card. The second has one shown and one hidden. The third has one shown and two hidden. Each stack has one more hidden card than the one before it, so the seventh stack, at the right, has one shown card and six hidden cards. There are 28 cards altogether on the board; the remaining 24 cards are in the hand.
Here are the legal moves:
I've expressed these rules in more formal language than would usually be used. Card players have shorthand ways of speaking, like "play up in the same suit at the top" or "play down in the opposite color on the stacks." I wanted to be very precise in stating the rules because each part of a rule must be reflected in the computer program. Even so, I've left out some details. For example, my list of rules talks about concepts like "suit" and "rank" without defining them. I haven't specified the rank order, namely ace-low. (That is, ace comes before two, not after king.) What other details, if any, have I forgotten?
To use the program, invoke the command solitaire with no inputs.
(Being as I am a lazy typist, I've also defined an abbreviation s
for this command.) The program prints an initial screenful of instructions,
and then repeatedly deals solitaire hands until you give the exit command.
Here are the instructions:
Welcome to solitaire
Here are the commands you can type:
+ = Deal three cards onto pile
P Play top card from pile
R Redisplay the board
? Retype these instructions
card Play that card
M Move same card again
W Play up as much as possible (Win)
G Give up (start a new game)
X Exit to Logo
A card consists of a rank:
A 2 3 4 5 6 7 8 9 10 J Q K or T for 10
followed by a suit:
H S D C
or followed by . to play all possible suits up
If you make a mistake, hit delete or backspace.
To move an entire stack,
hit the shifted stack number:
! @ # $ % ^ & for stacks
1 2 3 4 5 6 7
My goal in designing the "human interface" for this program was that most
moves should require typing only a single character. My idea is that the
most common moves are to play a card from the pile and to move an entire
stack (that is, the entire shown part of a stack) at once. There are
one-character commands for all these. If you want to move only part of a
stack, then you must type the name of the card, in the form 8S
for the eight of spades.
As it turns out, in this case what's easy for the user is also easiest for
the program. When you refer to a card by its position, it's easy for the
program to look up which card you mean. For example, when you say
P to play the top card from the pile, it's easy for the program
to find out what card that is. But when you specify a card by typing its
rank and suit, it's harder for the program to know where that card
is. The program must check the pile and all the stacks to see if your card
is a member of each one. So the program runs faster if you use the
single-keystroke commands.
The instructions don't say how to let the program know where you want to
move the chosen card onto. The reason is that in most cases there is
only one possible place, and the program finds that place itself. (This is
the most complicated part of the program.) Sometimes the chosen card can be
moved to two different places. If so, the program picks a stack to move the
card onto, and if you don't like the program's choice, you can type
M to move the same card again until it ends up where you wanted
it.
The program makes no effort to help you with strategic decisions. For
example, some people like to play cards to the top as soon as possible,
while other people prefer to keep cards visible on the stacks as long as
possible. Such choices are up to you. Also, the program does not detect
losing the game. (Detecting winning is easy--all four tops have kings
showing--but you haven't lost the game until no further moves are possible,
which is harder for the program to figure out.) When you decide the game is
over, you just type G to start another game.
There are about 60 procedures in this program. These procedures can be roughly divided into several purposes:
In the procedures that move cards, the most interesting part of the program, a few important variables are used to communicate what moves should be made:
cardcardswhereonto
As we'll see later in more detail, the card locations in :where
and :onto are represented in the form of Logo instructions that
can be run to perform the desired move.
The overall program structure is two nested loops. The top-level procedure
solitaire
repeatedly invokes onegame. As its name
suggests, each invocation of onegame
plays one solitaire game.
It shuffles and deals the cards, then repeatedly invokes
parsecmd,
which reads a character from the keyboard and chooses
the appropriate procedure to carry out the user's command.
(Most user commands require only one character. The situation is a little
more complicated if the user types the name of a card, such as
10H for the ten of hearts, as a command. Parsecmd
actually treats this as three separate commands. The 1 and the
0 merely record the card's rank in a variable named
digit. When parsecmd sees the letter
H, which selects the card's suit, it invokes
play.by.name, which combines the remembered rank with the
just-typed suit to determine the desired card.)
Both solitaire and onegame include initialization
instructions. That's because some actions are only required once, such as
computing the 52 names of cards in the deck, while others are required for
each game, such as shuffling those cards.
Many initialization actions use the Berkeley Logo primitive command
localmake, which is an abbreviation for a local
command followed by a make command. The program uses no global
variables, although the variables that are local to these top-level
procedures are available to any procedure within the solitaire program.
For most purposes, the most convenient representation of the deck of cards
is as a list. That's because what the program most often does with the deck
is to deal a card from it to somewhere else. If the deck is represented as
a list in the variable hand, then dealing a card is roughly
equivalent to these instructions:
do.something.with first :hand make "hand butfirst :hand
A list is convenient because butfirst can be used to remove a
card from the deck. It turns out, however, that shuffling the deck
is easiest if it's represented as an array. That's because the technique
used to shuffle the deck is to exchange pairs of cards repeatedly. In the
first step, we swap the 52nd card of the deck with a randomly chosen card
(perhaps itself). The newly chosen last card is now exempt from further
exchanges. In the second step, the 51st card of the deck is swapped with
some card in the remainder of the deck, and so on, for 51 steps. The
setitem primitive makes it easy to change the value of a member
partway through an array. If the deck were represented as a list, each
exchange would require making a (slightly changed) copy of the entire list.
The solution to this problem is that both representations, list and array,
are used in the program. The solitaire procedure creates an
array containing the 52 cards. For each game, onegame invokes
shuffle, which shuffles the cards in the array and then uses
the primitive arraytolist to output a list containing the cards
in their new order. That list is used by the other parts of the program.
to shuffle :len :array if :len=0 [output arraytolist :array] localmake "choice random :len localmake "temp item :choice :array setitem :choice :array (item :len-1 :array) setitem :len-1 :array :temp output shuffle :len-1 :array end
As in most large programs, the solitaire program uses selectors like
first and last for several different purposes in
different contexts. To make the program easier to read and maintain, more
meaningful names are used in each context.
For example, cards are represented in the program as words containing the
rank and the suit, so the word 8C represents the eight of
clubs. To find the rank of a card, the program must take the
butlast of the word, and to find the suit, it must take the
last of the word. (Why not use first instead of
butlast to get the rank? Because if the card happens to be a
ten, there are two digits in its rank. The suit is always a single
character.) Instead of using these primitive selectors directly, I've
defined synonyms:
to rank :card output butlast :card end to suit :card output last :card end
When considering playing a card onto a stack, the program does not have to know the precise suit of the card, but must know whether it's red or black:
to redp :card output memberp (suit :card) :reds end
One complication in dealing with cards is that the program wants to use a
card's rank in two different ways. For user interaction (reading commands
and displaying cards on the screen) the ranks should be represented using
the names for aces and picture cards (A, J,
Q, and K). But for comparison purposes (such as
deciding whether a card can be played on top of another card), it's more
convenient to represent all ranks as numbers: 1 for ace, 11 for jack, 12 for
queen, and 13 for king. A conversion function ranknum makes
this possible:
to ranknum :rank if emptyp :rank [output 0] if numberp :rank [output :rank] if :rank = "A [output 1] if :rank = "J [output 11] if :rank = "Q [output 12] if :rank = "K [output 13] end
(When would a rank be empty? The emptyp test is useful in
the case of deciding whether a card can be played onto an empty "top."
In general, the only card that can be played onto a top is the rank after
the one that's already visible there; for example, if a five is showing,
then a six can be played. Treating an empty top as having a rank of zero
means that the following rank, an ace, is permitted, just as the rules
require.)
In an actual solitaire game, a top is a pile of several cards of the same
suit, with an ace on the bottom and other cards over it in sequence. But in
the program, there is no need to represent any but the topmost card, since
the lower cards have no further role in the game. In this program, the tops
are represented by four variables toph, tops,
topd, and topc. (The last letter indicates the
suit.) The value of each variable is the empty word if that top is empty,
or the rank of the topmost card if not. Instead of using these variables
directly, the program uses data abstraction procedures top and
settop to examine and modify the values:
to top :suit output thing word "top :suit end to settop :suit :value make (word "top :suit) :value end
For example, part of the initialization in onegame is to
make all four tops empty:
foreach :suits [settop ? "]
A stack (also called a pushdown list) is a data structure that is used to remember things and recall them later. A stack uses the rule "Last In, First Out." That is, when you take something out of a stack, the one you get is the one you put in most recently. The name "stack" is based on the metaphor of the spring-loaded stack of trays you find in a self-service cafeteria. You add a tray to the stack by pushing down the trays that were already there, adding the new tray at the top of the pile. When you remove a tray, you take the one at the top of the pile--the one most recently added to the stack.
A pile of cards in a solitaire game works just like a pile of trays in a cafeteria. You add cards to the top of the pile, and you remove cards from the top of the pile. I've used the name "stack" for some of the piles of cards in this project partly because those groups of cards are represented in the program by stacks in the technical sense.
Berkeley Logo provides primitive procedures push and
pop to implement stacks. Each stack is represented as a list.
To push something onto the stack, Logo uses fput; to pop
something off the stack, it uses first. (Actually, it's
slightly more complicated, as you'll see in a moment. But this is
essentially true.) For example, each of the seven numbered card stacks in
the solitaire layout is represented by two lists, one for the shown cards
and one for the hidden cards. The lists for the third stack are kept in
variables named shown3 and hidden3. To
push a new card onto the hidden stack without using the
push primitive, you could say
make "hidden3 fput :card :hidden3
To pop a card from that stack, you'd say
make "card first :hidden3 make "hidden3 butfirst :hidden3
In this case, the first instruction reads the top of the stack, while the second removes that entry from the stack.
Berkeley Logo provides push and pop as a data
abstraction mechanism. Push is a command that takes two
inputs. The first input is a word, the name of a stack. The
second input is any Logo datum. Pop is an operation with one
input, the name of a stack. Its output is the first datum on the stack. It
also has the effect of removing that datum from the stack. Instead of the
instructions above, you can say
push "hidden3 :card make "card pop "hidden3
If Berkeley Logo didn't already provide these procedures, it would be easy to write them:
to push :stack :thing make :stack fput :thing (thing :stack) end to pop :stack local "result make "result first thing :stack make :stack butfirst thing :stack output :result end
Within the definition of push, the expression
:stack represents the name of the stack, while the expression
thing :stack represents the stack itself. The
make instruction is an example of indirect assignment; it does
not give a new value to the variable stack but rather to the
variable whose name is contained in stack.
Pop is an unusual Logo procedure in that it's an operation that
also has an effect. Most operations don't have effects. They compute
some value, but they don't make any permanent change in the state of the
computer. Another way of looking at this is to say that for most
operations, if you apply the same operation to the same inputs repeatedly,
you'll get the same result every time.
? make "cards [AH 5C 10S] ? print first :cards AH ? print first :cards AH ? print first :cards AH
But if you apply pop to the same input repeatedly, you'll
get a different output each time.
? print pop "cards AH ? print pop "cards 5C ? print pop "cards 10S
The combination of output and effect in pop is a powerful
technique, but a potentially confusing one. It's important for anyone who
tries to read this program to be aware that pop has an effect.
Fortunately, the concept of a stack is a standard, well-known convention in
computer science, and the names push and pop are
the traditional ones for this purpose, so pop is somewhat
self-documenting.
Before a stack can be used, it must be initialized. Generally a stack
starts out with no data in it. That is, it's initially an empty list. This
initialization could be done with an explicit make instruction,
but instead I invented a procedure for the purpose:
to setempty :stack make :stack [] end
I think this makes the program slightly more elegant.
It is an error to try to pop more items from a stack than you've pushed onto it. If you try to do this, you'll get an error message something like
First doesn't like [] as input
Often the logic of a program ensures automatically that you never try to overpop a stack. But in the solitaire program I sometimes have to check for this possibility explicitly, with an instruction like
if not emptyp :hidden3 [make "card pop "hidden3]
I've been using the name hidden3 as an example in this
discussion, typing "hidden3 when the name of the stack was
needed or :hidden3 when its value was needed. In fact, such
names do not appear explicitly in the program. There are no instructions
that are directed exclusively to the third stack. Instead, stack
instructions are applied either to all seven stacks or to a stack chosen by
the user through keyboard commands. The name of a stack must be
computed using an expression like
word "hidden :num
The contents of the stack would be examined by applying thing
to that expression. To make the program cleaner I created procedures to
generate these variable names.
to shown :num output word "shown :num end to hidden :num output word "hidden :num end
Remember that these operations output the name of a stack variable, not the contents of a stack. So, for example, you can use them in instructions like these:
push (shown 5) :card make "card pop shown 5 setempty shown 5
There are only a few places in the program where a procedure needs to refer
to the entire contents of a stack, rather than just pushing or popping a
single datum at a time. (One such place, for example, is
remshown, which has the job of removing perhaps several cards
from a stack.) In those places, there is an explicit use of
thing to examine the contents of a stack selected by
shown or hidden. An expression that occurred
often in the program was
emptyp thing shown :num
to see if a stack is empty; I cleaned up these expressions somewhat by inventing a special procedure for this test.
to stackemptyp :name output emptyp thing :name end
This is used in an expression like
stackemptyp shown :num
Note that when a stack is mentioned explicitly by name in the
program, like :hand or :pile, it is tested for
emptiness with the ordinary emptyp. In this case the colon
abbreviates the invocation of thing; for the shown
or hidden names, stackemptyp abbreviates the
invocation of thing.
One small detail that's easy to miss is that in a non-computer game of solitaire, when a hand is completely dealt out, you pick up the pile from the table and turn it over to form a new hand. What was the top card of the pile becomes the bottom card of the hand. The program achieves the same effect while dealing cards:
to deal if emptyp :hand [make "hand reverse :pile setempty "pile] if emptyp :hand [output []] output pop "hand end
The Berkeley Logo primitive operation reverse is used
to reverse the order of the cards as they are moved from the pile to
the hand.
In order for the program to move a card, it must first make sure that the
requested move is legal. The first step is to find the card's current
position. (That's easy if the move is requested by position, using the
P command to play the card at the top of the pile, or a shifted
stack number to move the entire shown stack; it's a little harder if the
card is requested by its rank and suit. Even then, in order to be playable
the card must be either on top of the pile or somewhere in a shown stack.)
The next step is to look for another position into which the card can be
moved; the only possibilities are a stack or a top. Only after both old and
new positions have been verified can the program actually modify its data
structures (and the screen display) to move the card.
When you type a card-moving command, parsecmd invokes one of
three procedures: playpile for the P command,
playstack for one of the shifted stack numbers (such as
# for stack 3), or play.by.name for a rank and
suit (such as 7D). The first two of these must figure out
which card is desired, and ensure that there is in fact a card in the
requested position; play.by.name has the opposite job, since it
already knows the card and must determine that it's in a playable position.
But in either case, these procedures do not actually move the card. They
ensure that the variable card has the desired card as its
value, and that the variable where has as its value a
representation of the card's current position. Then they call
playcard, whose job is to ensure that there is a valid
destination for the card, and if so, to move it:
to playcard
setempty "onto
if not coveredp [checktop]
if and not :upping ~
or (emptyp :onto) (not upsafep rank :card) ~
[checkonto]
if emptyp :onto [bell]
run :where
run first :onto
end
Subprocedures checktop and checkonto determine
whether the requested card can be moved to the top or to a stack. (Each of
these is called only if certain conditions are met. For
checktop, the condition is that the desired card must not be in
the middle of a shown stack; it must be either the bottommost card of a
shown stack or visible on the pile. The condition for calling
checkonto is more complicated. If the user's command was
. or W, then cards are played only into the top,
so there is no need to check the stacks. In other cases, to make the game
move more quickly, the program will always move the card to the top if it is
both possible and safe to do so. Such a move is considered safe if
every card whose rank is less than that of the requested card by two or more
is already in the top, because then any card of rank one less than the
chosen card can be played to the top, and so the chosen card is not needed
in the stacks.)
Just as :where identifies the card's current position,
:onto will hold all of the possible destination positions.
Checktop and checkonto add possible positions to
this variable, which is a list. If :onto is empty after
checktop and checkonto have been invoked, then
there is no legal way to move this card.
I want to focus attention on the two run instructions. They
are the ones that actually do the work of moving a card from one place to
another; the first removes the card from its original position and the
second inserts the card at its new position.
The value of the variable where is not merely a number or word
indicating where the card is to be found, but a Logo instruction that
invokes the procedure needed to remove the card. For example, suppose you
type the letter P to play a card from the top of the pile.
Parsecmd then invokes playpile:
to playpile if emptyp :pile [bell] if not emptyp :digit [bell] make "card first :pile make "where [rempile] carddis :card playcard end
The first two instructions check for errors. The first checks for trying to
play a card from the pile when there are no cards in the pile. The second
checks for the syntax error of typing a rank and then typing
P instead of a suit. Having cleared those hurdles, the next
instruction finds the actual card (rank and suit) you want to play from the
pile. The interesting part for the present discussion is that the variable
where is given as its value the list
[rempile]
Rempile is the name of a procedure with no inputs, so this
list contains a valid Logo instruction. The corresponding instruction in
playstack1 is
make "where sentence "remshown :num
which gives where a value like
[remshown 4]
if you've selected stack four. In either case, playcard can
later remove the card from its original location just by running
:where. At the same time, this Logo instruction can
be examined as a datum. For example, coveredp contains
the instruction
if equalp :where [rempile] [output "false]
Most programming languages don't have a facility like Logo's
run command. In those languages, the variable
where would have to contain, for example, a number indicating
where the card is to be found. Playcard would then use this
number to choose a course of action with a series of instructions like this:
if :where = 0 [rempile] if :where = 1 [remshown 1] if :where = 2 [remshown 2]
... and so on.
The situation concerning the variable onto is similar, except
that there is a slight complication because there may be more than one legal
destination for a card. (By contrast, every card starts out in exactly one
place!) Therefore, checktop and checkonto set up
:onto as a list of Logo instructions, one for every
possible destination. If a card could be played onto stack 3, stack 6, or
the top, :onto will be
[[playonto 3] [playonto 6] [playtop]]
Playcard runs the first member of this list. Why bother saving
the other members? After a successful move, the user can type
M to move the same card to a different destination. Here's how
that is done:
to again if not emptyp :digit [bell] if emptyp :onto [bell] make "where list "remshown last pop "onto if emptyp :onto [bell] carddis :card run :where run first :onto end
This procedure uses the values that are still left over in
:card and :onto from the last move. The first
member of :onto is the instruction that moved the card onto a
stack. (If the card was moved to the top, it's because there were no
alternatives in :onto, because playtop is always
the last choice in the list.) That stack is now the card's position of
origin! If :onto was
[[playonto 3] [playonto 6] [playtop]]
then the instruction
make "where list "remshown last pop "onto
will give where the value
[remshown 3]
and, because pop removes the first datum from the stack,
leaves onto with the value
[[playonto 6] [playtop]]
The chosen card will be moved from stack three to stack six. If the user
types M again, then the card will be moved from stack six to
the top.
Consider the procedure that interprets what you type at the keyboard while running the solitaire program:
to parsecmd ;; abbreviated version local "char make "char uppercase readchar if equalp :char "T [parsedigit 1 parsezero stop] if memberp :char [1 2 3 4 5 6 7 8 9 A J Q K] [parsedigit :char stop] if equalp :char "0 [parsezero stop] if memberp :char :suits [play.by.name :char stop] if equalp :char ". [allup stop] if equalp :char "W [wingame stop] if equalp :char "M [again stop] ; several more possibilities omitted... bell end
This sort of thing is common in Logo programming: a string of
ifs in which each conditional instruction list ends with
stop because the choices are mutually exclusive.
Some people find this use of stop offensive because it doesn't
make it graphically apparent when reading the program that the choices are
exclusive. The form of the program makes it seem that each decision (that
is, each if instruction) is independent of the others.
It would be possible to meet this objection by using ifelse,
putting each new test in the false part of the previous one:
to parsecmd
local "char
make "char uppercase readchar
ifelse equalp :char "T ~
[parsedigit 1 parsezero]
[ifelse memberp :char [1 2 3 4 5 6 7 8 9 A J Q K]
[parsedigit :char]
[ifelse equalp :char "0 [parsezero]
; ...
bell]]
end
It's not clear that this is an improvement, although the use of
ifelse makes more sense as an alternative to
stop when only a single decision is involved.
Some programming languages provide a special representation for such a multiple branching decision. A Logo equivalent might look like this:
to parsecmd local "char make "char uppercase readchar branch [ [[equalp :char "T] [parsedigit 1 parsezero]] [[memberp :char [1 2 3 4 5 6 7 8 9 A J Q K]] [parsedigit :char]] [[equalp :char "0] [parsezero]] [[memberp :char :suits] [play.by.name :char]] [[equalp :char ".] [allup]] [[equalp :char "W] [wingame]] [[equalp :char "M] [again]] ; several more possibilities omitted... [["true] [bell]] ] end
Branch is a hypothetical command that takes a single input, a
list of lists. Each member of the input is a list with two members. The
first member must be a Logo predicate expression; the second must be a Logo
instruction. Branch evaluates the first half of each pair. If
the value is true, branch then carries out the
instruction in the second half of that pair, and then stops without
evaluating the remaining pairs. If the value is false,
branch goes on to the next pair. Branch is not a
Logo primitive, but it can easily be written in Logo:
to branch :conditions if emptyp :conditions [stop] if (run first first :conditions) [run last first :conditions stop] branch butfirst :conditions end
Inventing control structures like this is the sort of thing Logo makes easy and other languages make impossible.
The trouble with this particular control structure in Logo is that the input
to branch is typically a very long list, extending over several
lines on the screen. Traditional Logo dialects have not done a good job of
presenting such long lists with clear formatting. More recent versions can,
however, handle instructions like that multi-line branch
invocation.
I keep thinking of new features I'd like in this program. I think the most important is an Undo command, which would undo the effect of the previous user command. This should be pretty easy to implement; every time the program changes the value of a variable that represents card positions, it should make a list of the variable's name and its old value, and push that onto a changes list. For example, here's the procedure that removes a card from the pile:
to rempile make "cards (list (pop "pile)) dispile end
And here's how I'd change it for the undo command:
to rempile push "undo.list (list "pile :pile) make "cards (list (pop "pile)) dispile end
The undo command itself would go through the list, restoring the values of
all the variables it finds, and then call redisplay to make the
display match the program's state. Playcard would
setempty the undo list before moving any cards.
Another possibility is to improve the display. One person who tried this program commented that it's not enough to indicate whether the hidden part of a stack is empty or nonempty; he wanted to see exactly how many cards are present. Novice users might be helped by keeping an abbreviated command list in the empty space toward the right side of the screen.
A more ambitious direction you could pursue is to write a similar program for a different solitaire game. There are books of card games that include several variations on this kind of solitaire as well as versions of solitaire that are totally different in their rules and layouts.
Another direction would be to try to have the program offer strategic suggestions, or even play the game entirely by itself. As with any strategy game, you would have to choose between determining the strategy for the program in advance and letting it learn from its experience and modify its strategy. Which is better, playing cards to the top quickly or saving them in the stacks as long as possible? Which is better, playing a card from the pile or playing a card of the same rank and color from the stacks? You could research these questions by writing versions of the program with different strategies and collecting statistics on their performance.
Another possibility would be to abandon solitaire and program the computer to play one side of a two-player game with you. Blackjack is a simple example; poker is a harder one.
A different kind of exploration would be to try to speed up the running of this program. Earlier I suggested the possibility that the program might benefit from remembering explicitly the position of each card. You could find out whether or not that would really help. (It would speed up the searching process for a card, but it would also slow down the moving of cards because the program would have to remember the new location instead of the old one. My guess is that the speedup would be substantial and the slowdown minimal, but I'm not sure.) What other bottlenecks can you find in this program, and how can you improve them?
| (back to Table of Contents) | BACK chapter thread NEXT |
If you trace the progress of a user command, let's say P to
play from the pile, from parsecmd through playpile
and playcard to rempile and then either
playtop or playonto, you'll understand most of the
program. There are a few slightly complicated details in moving several
cards from one stack to another (remshown and
playonto) but nothing really hard to understand.
to solitaire
print [Welcome to solitaire]
instruct
localmake "allranks [A 2 3 4 5 6 7 8 9 10 J Q K]
localmake "numranks map "ranknum :allranks
localmake "suits [H S D C]
localmake "reds [H D]
localmake "deckarray (listtoarray (crossmap "word :allranks :suits) 0)
localmake "upping "false
catch "exit [forever [onegame cleartext]]
cleartext
end
to s
solitaire
end
to onegame
print [Shuffling, please wait...]
local [card cards digit pile where]
localmake "onto []
local map [word "top ?] :suits
local cascade 9 [(sentence (word "shown #) (word "hidden #) ?)] []
localmake "ranks :allranks
localmake "numstacks 7
local map [word "num ?] :numranks
foreach :numranks [make word "num ? 4]
localmake "hand shuffle 52 :deckarray
setempty "pile
initstacks
foreach :suits [settop ? "]
redisplay
catch "endgame [forever [catch "bell [parsecmd]]]
end
;; Initialization
to instruct
print [] print [Here are the commands you can type:]
type "| | type (sentence standout "+ standout "=)
type "| | print [Deal three cards onto pile]
instruct1 "P [Play top card from pile]
instruct1 "R [Redisplay the board]
instruct1 "? [Retype these instructions]
instruct1 "card [Play that card]
instruct1 "M [Move same card again]
instruct1 "W [Play up as much as possible (Win)]
instruct1 "G [Give up (start a new game)]
instruct1 "X [Exit to Logo]
print [A card consists of a rank:]
type "| | print (sentence standout [A 2 3 4 5 6 7 8 9 10 J Q K]
"or standout "T [for 10])
print [followed by a suit:]
type "| | print standout [H S D C]
print (sentence [or followed by] standout ".
[to play all possible suits up])
print [] print [If you make a mistake, hit delete or backspace.]
print [] print [To move an entire stack,]
type "| | print [hit the shifted stack number:]
type "| | print (sentence standout [! @ # $ % ^ &] [for stacks])
type "| | print [1 2 3 4 5 6 7]
print []
end
to instruct1 :key :meaning
type "| |
type standout :key
repeat 5-count :key [type "| |]
print :meaning
end
to shuffle :len :array
if :len=0 [output arraytolist :array]
localmake "choice random :len
localmake "temp item :choice :array
setitem :choice :array (item :len-1 :array)
setitem :len-1 :array :temp
output shuffle :len-1 :array
end
to initstacks
for [num 1 7] [inithidden :num
turnup :num]
end
to inithidden :num
localmake "name hidden :num
setempty :name
repeat :num [push :name deal]
end
;; Reading and interpreting user commands
to parsecmd
if emptyp :digit [setcursor [1 22] type "| | setcursor [1 22]]
local "char
make "char uppercase readchar
if equalp :char "T [parsedigit 1 parsezero stop]
if memberp :char [1 2 3 4 5 6 7 8 9 A J Q K] [parsedigit :char stop]
if equalp :char "0 [parsezero stop]
if memberp :char :suits [play.by.name :char stop]
if equalp :char ". [allup stop]
if equalp :char "W [wingame stop]
if equalp :char "M [again stop]
if memberp :char [+ =] [hand3 stop]
if equalp :char "R [redisplay stop]
if equalp :char "? [helper stop]
if equalp :char "P [playpile stop]
if and equalp :char "|(| not emptyp :digit [cheat stop]
if and equalp :char "|)| not emptyp :digit [newstack stop]
if memberp :char [! @ # $ % ^ & * ( )] ~
[playstack :char [! @ # $ % ^ & * ( )] stop]
if memberp :char (list "| | char 8 char 127) [rubout stop]
if equalp :char "G [throw "endgame]
if equalp :char "X [throw "exit]
bell
end
to parsedigit :char
if not emptyp :digit [bell]
make "digit :char
type :digit
end
to parsezero
if not equalp :digit 1 [bell]
make "digit 10
type 0
end
to rubout
setcursor [1 22]
type "| |
setcursor [1 22]
setempty "digit
end
to bell
if not :upping [type char 7]
setempty "digit
throw "bell
end
;; Deal three cards from the hand
to hand3
if not emptyp :digit [bell]
if and emptyp :hand emptyp :pile [bell]
push "pile deal
repeat 2 [if not emptyp :hand [push "pile deal]]
dispile dishand
end
to deal
if emptyp :hand [make "hand reverse :pile setempty "pile]
if emptyp :hand [output []]
output pop "hand
end
;; Select card to play by position (pile or stack) or by name
to playpile
if emptyp :pile [bell]
if not emptyp :digit [bell]
make "card first :pile
make "where [rempile]
carddis :card
playcard
end
to playstack :which :list
if not emptyp :digit [bell]
foreach :list [if equalp :which ? [playstack1 # stop]]
end
to playstack1 :num
if greaterp :num :numstacks [bell]
if stackemptyp shown :num [bell]
make "card last thing shown :num
make "where sentence "remshown :num
carddis :card
playcard
end
to play.by.name :char
if emptyp :digit [bell]
if equalp :digit 1 [make "digit "a]
type :char
wait 0
make "card word :digit :char
setempty "digit
findcard
if not emptyp :where [playcard]
end
to findcard
if findpile [stop]
make "where findshown
if emptyp :where [bell]
end
to findpile
if emptyp :pile [output "false]
if equalp :card first :pile [make "where [rempile] output "true]
output "false
end
to findshown
for [num 1 :numstacks] ~
[if memberp :card thing shown :num [output sentence "remshown :num]]
output []
end
;; Figure out all possible places to play card, then pick one
to playcard
setempty "onto
if not coveredp [checktop]
if and not :upping ~
or (emptyp :onto) (not upsafep rank :card) ~
[checkonto]
if emptyp :onto [bell]
run :where
run first :onto
end
to coveredp
if equalp :where [rempile] [output "false]
output not equalp :card first thing shown last :where
end
to upsafep :rank
if memberp :rank [A 2] [output "true]
output equalp 0 thing word "num ((ranknum :rank)-2)
end
to checktop
if (ranknum rank :card) = 1 + (ranknum top suit :card) ~
[push "onto (list "playtop word "" suit :card)]
end
to checkonto
for [num :numstacks 1] ~
[ifelse stackemptyp shown :num
[checkempty :num]
[checkfull :num thing shown :num]]
end
to checkempty :num
if equalp rank :card "k [push "onto (list "playonto :num)]
end
to checkfull :num :stack
if equalp (redp :card) (redp first :stack) [stop]
if ((ranknum rank first :stack) = 1 + (ranknum rank :card)) ~
[push "onto (list "playonto :num)]
end
;; Play card, step 1: remove from old position
to rempile
make "cards (list (pop "pile))
dispile
end
to remshown :num
setempty "cards
remshown1 :num (count thing shown :num)
if stackemptyp shown :num [turnup :num disstack :num]
end
to remshown1 :num :length
do.until [push "cards (pop shown :num)] ~
[equalp :card first :cards]
for [i 1 [count :cards]] ~
[setcursor list (5*:num - 4) (5+:length-:i) type "| |]
end
to turnup :num
setempty shown :num
if stackemptyp hidden :num [stop]
push (shown :num) (pop hidden :num)
end
;; Play card, step 2: put in new position
to playtop :suit
localmake "var word "num ranknum rank :card
settop :suit rank :card
distop :suit
make :var (thing :var)-1
if (thing :var)=0 [make "ranks butfirst :ranks]
end
to playonto :num
localmake "row 4+count thing shown :num
localmake "col 5*:num-4
for [i 1 [count :cards]] ~
[localmake "card pop "cards
push (shown :num) :card
setcursor list :col :row+:i
carddis :card]
end
;; Update screen display
to redisplay
cleartext
for [num 1 :numstacks] [disstack :num]
foreach :suits "distop
dispile
dishand
setcursor [1 22]
setempty "digit
end
to disstack :num
setcursor list (-3 + 5 * :num) 4
type ifelse stackemptyp hidden :num ["| |] ["-]
if stackemptyp shown :num [setcursor list (-4 + 5 * :num) 5
type "| | stop]
localmake "stack (thing shown :num)
localmake "col 5*:num-4
for [i [count :stack] 1] ~
[setcursor list :col :i+4
carddis pop "stack]
end
to distop :suit
if emptyp top :suit [stop]
if equalp :suit "H [distop1 4 stop]
if equalp :suit "S [distop1 11 stop]
if equalp :suit "D [distop1 18 stop]
distop1 25
end
to distop1 :col
setcursor list :col 2
carddis word (top :suit) :suit
end
to dispile
setcursor [32 23]
ifelse emptyp :pile [type "| |] [carddis first :pile]
end
to dishand
setcursor [27 23]
type count :hand
type "| |
end
to carddis :card
ifelse memberp suit :card :reds [redtype :card] [blacktype :card]
type "| |
end
to redtype :word
type :word
end
to blacktype :word
type standout :word
end
;; Miscellaneous user commands
to again
if not emptyp :digit [bell]
if emptyp :onto [bell]
make "where list "remshown last pop "onto
if emptyp :onto [bell]
carddis :card
run :where
run first :onto
end
to allup
if emptyp :digit [bell]
if equalp :digit 1 [make "digit "a]
localmake "upping "true
type ". wait 0
foreach map [word :digit ?] [H S D C] ~
[catch "bell [make "card ?
findcard
if not emptyp :where [playcard]]]
setempty "digit
end
to helper
cleartext
instruct
print standout [type any key to continue]
ignore rc
redisplay
end
to wingame
type "W
localmake "cursor cursor
foreach :ranks [if not upsafep ? [stop]
make "digit ? ~
allup ~
setempty "digit ~
setcursor :cursor]
if equalp (map "top [H S D C]) [K K K K] ~
[ct print [you win!] wait 120 throw "endgame]
end
to newstack
localmake "num :numstacks+1
setcursor [1 22] type "| |
if not equalp :digit 9 [bell]
setempty hidden :num
setempty shown :num
make "numstacks :num
setempty "digit
end
to cheat
setcursor [1 22] type "| |
if not equalp :digit 8 [bell]
if and emptyp :hand emptyp :pile [bell]
push "pile deal
dispile
dishand
setempty "digit
end
;; Data abstraction (ranks)
to rank :card
output butlast :card
end
to ranknum :rank
if emptyp :rank [output 0]
if numberp :rank [output :rank]
if :rank = "A [output 1]
if :rank = "J [output 11]
if :rank = "Q [output 12]
if :rank = "K [output 13]
end
;; Data abstraction (suits)
to suit :card
output last :card
end
to redp :card
output memberp (suit :card) :reds
end
;; Data abstraction (tops)
to top :suit
output thing word "top :suit
end
to settop :suit :value
make (word "top :suit) :value
end
;; Data abstraction (card stacks)
to shown :num
output word "shown :num
end
to hidden :num
output word "hidden :num
end
;; Data abstraction (pushdown stacks)
to stackemptyp :name
output emptyp thing :name
end
to setempty :stack
make :stack []
end
Brian Harvey,
bh@cs.berkeley.edu