| Brian
Harvey University of California, Berkeley |
| Download PDF version |
| Back to Table of Contents |
| BACK chapter thread NEXT |
| MIT Press web page for Computer Science Logo Style |
|
|
Program file for this chapter: pascal
We are now ready to turn from the questions of language design to those of compiler implementation. A Pascal compiler is a much larger programming project than most of the ones we've explored so far. You might well ask, "where do we begin in writing a compiler?" My goal in this chapter is to show some of the parts that go into a compiler design.
A compiler translates programs from a language like Pascal into the machine language of some particular computer model. My compiler translates into a simplified, simulated machine language; the compiled programs are actually carried out by another Logo program, the simulator, rather than directly by the computer hardware. The advantage of using this simulated machine language is that this compiler will work no matter what kind of computer you have; also, the simplifications in this simulated machine allow me to leave out many confusing details of a practical compiler. Our machine language is, however, realistic enough to give you a good sense of what compiling into a real machine language would be like; it's loosely based on the MIPS microprocessor design. You'll see in a moment that most of the structure of the compiler is independent of the target language, anyway.
Here is a short, uninteresting Pascal program:
program test;
procedure doit(n:integer);
begin
writeln(n,n*n)
end;
begin
doit(3)
end.
If you type this program into a disk file and then compile it
using compile as described in Chapter 4, the compiler will translate
the program into this sequence of instructions, contained in a list in the
variable named %test:
[ [add 3 0 0]
[add 4 0 0]
[addi 2 0 36]
[jump "g1]
%doit [store 1 0(4)]
[jump "g2]
g2 [rload 7 36(4)]
[putint 10 7]
[rload 7 36(4)]
[rload 8 36(4)]
[mul 7 7 8]
[putint 10 7]
[newline]
[rload 1 0(4)]
[add 2 4 0]
[rload 4 3(2)]
[jr 1]
g1 [store 5 1(2)]
[add 5 2 0]
[addi 2 2 37]
[store 4 3(5)]
[store 4 2(5)]
[addi 7 0 3]
[store 7 36(5)]
[add 4 5 0]
[rload 5 1(4)]
[jal 1 "%doit]
[exit]
]
I've displayed this list of instructions with some extra spacing
thrown in to make it look somewhat like a typical assembler listing.
(An assembler is a program that translates a notation like add 3 0 0
into a binary number, the form in which the machine hardware actually
recognizes these instructions.) A real assembler listing wouldn't have the
square brackets that Logo uses to mark each sublist, but would instead
depend on the convention that each instruction occupies one line.
The first three instructions carry out initialization that would be the same
for any compiled Pascal program; the fourth is a jump instruction that
tells the (simulated) computer to skip to the instruction following the
label g1 that appears later in the program. (A word that
isn't part of a sublist is a label.) In Pascal, the body of the main
program comes after the declarations of procedures; this jump
instruction allows the compiler to translate the parts of the program in the
order in which they appear.
(Two instructions later, you'll notice a jump to a label that comes
right after the jump instruction! The compiler issues this useless
instruction just in case some internal procedures were declared within
the procedure doit. A better compiler would include an
optimizer that would go through the compiled program looking for
ways to eliminate unnecessary instructions such as this one. The optimizer
is the most important thing that I've left out of my compiler.)
We're not ready yet to talk in detail about how the compiled instructions
represent the Pascal program, but you might be able to guess certain things.
For example, the variable n in procedure doit seems to be
represented as 36(4) in the compiled program; you can see where
36(4) is printed and then multiplied by itself, although it may not yet be
clear to you what the numbers 7 and 8 have to do with anything.
Before we get into those details, I want to give a broader overview of
the organization of the compiler.
The compilation process is divided into three main pieces. First and
simplest is tokenization. The compiler initially sees the
source program as a string of characters: p, then r, and so on,
including spaces and line separators. The first step in compilation is to
turn these characters into symbols, so that the later stages of compilation
can deal with the word program as a unit. The second piece of the
compiler is the parser, the part that recognizes certain
patterns of symbols as representing meaningful units. "Oh," says the
parser, "I've just seen the word procedure so what comes next must be
a procedure header and then a begin-end block for the body of
the procedure." Finally, there is the process of
code generation, in which each unit that was recognized by the
parser is actually translated into the equivalent machine language
instructions.
(I don't mean that parsing and code generation happen separately, one after the other, in the compiler's algorithm. In fact each meaningful unit is translated as it's encountered, and the translation of a large unit like a procedure includes, recursively, the translation of smaller units like statements. But parsing and code generation are conceptually two different tasks, and we'll talk about them separately.)
One common starting place is to develop a formal definition for the language we're trying to compile. The regular expressions of Chapter 1 are an example of what I mean by a formal definition. A regular expression tells us unambiguously that certain strings of characters are accepted as members of the category defined by the expression, while other strings aren't. A language like Pascal is too complicated to be described by a regular expression, but other kinds of formal definition can be used.
The formal systems of Chapter 1 just gave a yes-or-no decision for any input string: Is it, or is it not, accepted in the language under discussion? That's not quite good enough for a compiler. We don't just want to know whether a Pascal program is syntactically correct; we want a translation of the program into some executable form. Nevertheless, it turns out to be worthwhile to begin by designing a formal acceptor for Pascal. That part of the compiler--the part that determines the syntactic structure of the source program--is called the parser. Later we'll add provisions for code generation: the translation of each syntactic unit of the source program into a piece of object (executable) program that carries out the meaning (the semantics) of that unit.
One common form in which programming languages are described is the production rule notation mentioned briefly in Chapter 1. For example, here is part of a specification for Pascal:
program: program identifier filenames ; block . filenames: | ( idlist ) idlist: identifier | idlist , identifier block: varpart procpart compound varpart: | var varlist procpart: | procpart procedure | procpart function compound: begin statements end statements: statement | statements ; statement procedure: procedure identifier args ; block ; function: function identifier args : type ; block ;
A program consists of six components. Some of these components
are particular words (like program) or punctuation marks; other
components are defined in terms of even smaller units by other
rules.*
*The filenames component is an optional list of
names of files, part of Pascal's input/output capability; my compiler doesn't
handle file input or output, so it ignores this list if there is one.
A vertical bar (|) in a rule separates alternatives; an idlist
(identifier list) is either a single identifier or a smaller idlist followed
by a comma and another identifier. Sometimes one of the alternatives in a
rule is empty; for example, a varpart can be empty because a block need not
declare any local variables.
The goal in designing a formal specification is to capture the syntactic hierarchy of the language you're describing. For example, you could define a Pascal type as
type: integer | real | char | boolean | array range of integer |
packed array range of integer | array range of real |
...
but it's better to say
type: scalar | array range of scalar |
packed array range of scalar
scalar: integer | real | char | boolean
Try completing the syntactic description of my subset of Pascal along these lines. You might also try a similar syntactic description of Logo. Which is easier?
Another kind of formal description is the recursive transition network (RTN). An RTN is like a finite-state machine except that instead of each arrow representing a single symbol in the machine's alphabet, an arrow can be labeled with the name of another RTN; such an arrow represents any string of symbols accepted by that RTN.
Below I show two RTNs, one for a program and one for a
sequence of statements (the body of a compound statement).
In the former, the transition from state 5 to state 6 is followed if what
comes next in the Pascal program is a string of symbols accepted by the RTN
named "block." In these diagrams, a word in typewriter style like
program represents a single symbol, as in a finite-state machine diagram,
while a word in italics like block represents any
string accepted by the RTN of that name. The statements RTN
is recursive; one path through the network involves a transition that
requires parsing a smaller statements unit.
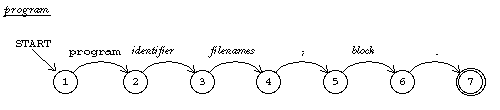
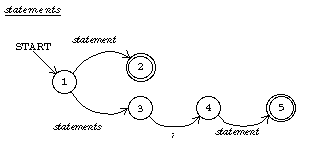
In both the production rules and the RTNs I've treated words like
program as a single symbol of the "alphabet" of the language. It would
be possible, of course, to use single characters as the alphabetic symbols
and describe the language in this form:
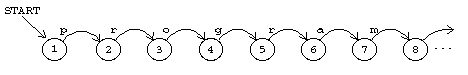
Extending the formal description down to that level, though, makes
it hard to see the forest for the trees; the important structural patterns
get lost in details about, for instance, where spaces are required between
words (as in program tower), where they're optional (as in
2 + 3), and where they're not allowed at all (prog
ram). A similar complication is that a comment in braces can
be inserted anywhere in the program; it would be enormously complicated if
every state of every RTN had to have a transition for a left brace beginning
a comment.
Most language processors therefore group the characters of the source
program into tokens used as the alphabet for the formal
grammar. A token may be a single character, such as a punctuation mark, or
a group of characters, such as a word or a number. Spaces do not ordinarily
form part of tokens, although in the Pascal compiler one kind of token is a
quoted character string that can include spaces. Comments are also removed
during tokenization. Here's what the tower program from Chapter 4
looks like in token form:

Tokenization is what the Logo readlist operation does when
it uses spaces and brackets to turn the string of characters you type into
a sequence of words and lists.
Tokenization is also called lexical analysis. This term has nothing to do with lexical scope; the word "lexical" is used not to remind us of a dictionary but because the root "lex" means word and lexical analysis divides the source program into words.
I've been talking as if the Pascal compiler first went through the entire
source file tokenizing it and then went back and parsed the result. That's
not actually how it works; instead, the parser just calls a procedure named
token whenever it wants to see the next token in the source file.
I've already mentioned that Pascal was designed to allow the compiler to
read straight through the source program without jumping around and
re-reading parts of it.
Consider the situation when the parser has recognized the first token
(program) as the beginning of a program and it invokes token to
read the second token, the program name. In the tower program, the
desired token is tower. Token reads the letter t; since
it's a letter, it must be the beginning of an identifier. Any number of
letters or digits following the t will be part of the identifier, but
the first non-alphanumeric character ends the token. (In this case, the
character that ends the token will be a semicolon.)
What this means is that token has to read one character too many in
order to find the end of the word tower. The semicolon isn't
part of that token; it's part of the following token. (In fact it's
the entire following token, but in other situations that need not be true.)
Ordinarily token begins its work by reading a character from the
source file, but the next time we call token it has to deal with the
character it's already read. It would simplify things enormously if
token could "un-read" the semicolon that ends the token
tower. It's possible to allow something like un-reading by using a
technique called lookahead.
to getchar
local "char
if namep "peekchar
[make "char :peekchar
ern "peekchar
output :char]
output readchar
end
Getchar is the procedure that token calls to read the next
character from the source file. Ordinarily getchar just invokes the
primitive readchar to read a character from the file.* But if there is a variable named peekchar, then
getchar just outputs whatever is in that variable without looking at the
file. Token can now un-read a character by saying
*I'm lying.
The real
getchar is slightly more complicated because it checks for an
unexpected end of file and because it prints the characters that it reads
onto the screen. The program listing at the end of the chapter tells the
whole story.
make "peekchar :char
This technique only allows token to un-read a single
character at a time. It would be possible to replace peekchar with a
list of pre-read characters to be recycled. But in fact one is
enough. When a program "peeks at" characters before they're read "for
real," the technique is called lookahead. Getchar uses
one-character lookahead because peekchar only stores a single
character.
It turns out that, for similar reasons, the Pascal parser will occasionally
find it convenient to peek at a token and re-read it later.
Token therefore provides for one-token lookahead using a similar
mechanism:
to token
local [token char]
if namep "peektoken [make "token :peektoken
ern "peektoken output :token]
make "char getchar
if equalp :char "|{| [skipcomment output token]
if equalp :char char 32 [output token]
if equalp :char char 13 [output token]
if equalp :char char 10 [output token]
if equalp :char "' [output string "']
if memberp :char [+ - * / = ( , ) |[| |]| |;|] [output :char]
if equalp :char "|<| [output twochar "|<| [= >]]
if equalp :char "|>| [output twochar "|>| [=]]
if equalp :char ". [output twochar ". [.]]
if equalp :char ": [output twochar ": [=]]
if numberp :char [output number :char]
if letterp ascii :char [output token1 lowercase :char]
(throw "error sentence [unrecognized character:] :char)
end
to twochar :old :ok
localmake "char getchar
if memberp :char :ok [output word :old :char]
make "peekchar :char
output :old
end
As you can see, token is mainly a selection of special cases.
Char 32 is a space; char 13 or char 10 is the end-of-line
character. Skipcomment skips over characters until it sees a right
brace. String accumulates characters up to and including a single
quote (apostrophe), except that two single quotes in a row become one single
quote inside the string and don't end the string. Number is a little
tricky because of decimal points (the string of characters 1.10 is a
single token, but the string 1..10 is three tokens!) and exponent
notation. I'm not showing you all the details because the compiler is a
very large program and we'll never get through it if I annotate every
procedure. But I did want to show you twochar because it's a good,
simple example of character lookahead at work. If the character < is
seen in the source program, it may be a token by itself or it may be part of
the two-character tokens <= or <>. Twochar takes a peek
at the next character in the file to decide.
If the character that token reads isn't part of any recognizable
token, the procedure generates an error. (The error is caught by the
toplevel procedure compile so that it can close the source file.)
This extremely primitive error handling is one of the most serious
deficiencies in my compiler; it would be better if the compilation process
continued, despite the error, so that any other errors in the program could
also be discovered. In a real compiler, more than half of the parsing
effort goes into error handling; it's relatively trivial to parse a correct
source program.
There are general techniques for turning a formal language specification, such as a set of production rules, into an algorithm for parsing the language so specified. These techniques are analogous to the program in Chapter 1 that translates a regular expression into a finite-state machine. A program that turns a formal specification into a parser is called a parser generator.
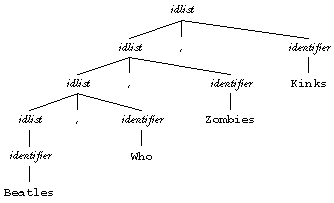
The trouble is that the techniques that work for any set of rules are quite slow. The time required to parse a sequence of length n is O(n2) if the grammar is unambiguous or O(n3) if it's ambiguous. A grammar is ambiguous if the same input sequence can be parsed correctly in more than one way. For example, if the production rule
idlist: identifier | idlist , identifier
is applied to the string
Beatles,Who,Zombies,Kinks
then the only possible application of the rule to accept the string produces this left-to-right grouping:
However, if the rule were
idlist: identifier | idlist , idlist
this new rule would accept the same strings, but would allow alternative groupings like
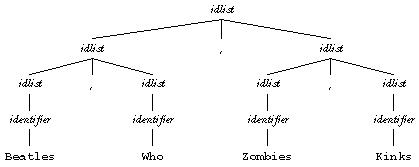
The former rule could be part of an unambiguous grammar; the new rule makes the grammar that contains it ambiguous.
It's usually not hard to devise an unambiguous grammar for any practical programming language, but even a quadratic algorithm is too slow. Luckily, most programming languages have deterministic grammars, which is a condition even stricter than being unambiguous. It means that a parser can read a program from left to right, and can figure out what to do with the next token using only a fixed amount of lookahead. A parser for a deterministic grammar can run in linear time, which is a lot better than quadratic.
When I said "figure out what to do with the next token," I was being
deliberately vague. A deterministic parser doesn't necessarily know exactly
how a token will fit into the complete program--which production rules will
be branch nodes in a parse tree having this token as a leaf node--as soon
as it reads the token. As a somewhat silly example, pretend that the word
if is not a "reserved word" in Pascal; suppose it could be the
name of a variable. Then, when the parser is expecting the beginning of a
new statement and the next token is the word if, the parser doesn't
know whether it is seeing the beginning of a conditional statement such as
if x > 0 then writeln('positive') or the beginning of an assignment
statement such as if := 87. But the parser could still be deterministic.
Upon seeing the word if, it would enter a state (as in a finite state
machine) from which there are two exits. If the next token turned out to be
the := assignment operator, the parser would follow one transition; if
the next token was a variable or constant value, the parser would choose a
different next state.
The real Pascal, though, contains no such syntactic cliffhangers. A Pascal
compiler can always tell which production rule the next token requires.
That's why the language includes keywords like var,
procedure, and function. For the most part, you could figure out
which kind of declaration you're reading without those keywords by looking
for clues like whether or not there are parentheses after the identifier
being declared. (If so, it's a procedure or a function.) But the keywords
let you know from the beginning what to expect next. That means we can
write what's called a predictive grammar for Pascal,
even simpler to implement than a deterministic one.
There are general algorithms for parsing deterministic languages, and there are parser generators using these algorithms. One widely used example is the YACC (Yet Another Compiler Compiler) program that translates production rules into a parser in the C programming language.* But because Pascal's grammar is so simple I found it just as easy to do the translation by hand. For each production rule in a formal description of Pascal, the compiler includes a Logo procedure that parses each component part of the production rule. A parser written in this way is called a recursive descent parser. Here's a sample:
*A parser
generator is also called a compiler compiler because it treats
the formal specification as a kind of source program and produces a compiler
as the object program. But the name isn't quite accurate because, as you
know, there's more to a compiler than the parser.
to statement local [token type] ifbe "begin [compound stop] ifbe "for [pfor stop] ifbe "if [pif stop] ifbe "while [pwhile stop] ifbe "repeat [prepeat stop] ifbe "write [pwrite stop] ifbe "writeln [pwriteln stop] make "token token make "peektoken :token if memberp :token [|;| end until] [stop] make "type gettype :token if emptyp :type [(throw "error sentence :token [can't begin statement])] if equalp :type "procedure [pproccall stop] if equalp :type "function [pfunset stop] passign end to pif local [cond elsetag endtag] make "cond pboolean pexpr make "elsetag gensym make "endtag gensym mustbe "then code (list "jumpf :cond (word "" :elsetag)) regfree :cond statement code (list "jump (word "" :endtag)) code :elsetag ifbe "else [statement] code :endtag end
Many of the details of pif have to do with code
generation, but never mind those parts now. For the
moment, my concern is with the parsing aspect of these procedures: how they
decide what to accept.
Statement is an important part of the parser; it is invoked whenever a
Pascal statement is expected. It begins by checking the next token from the
source file. If that token is begin, for, if, while,
or repeat then we're finished with the token and statement turns
to a subprocedure to handle the syntax of whatever structured statement type
we've found. If the token isn't one of those, then the statement has to be
a simple statement and the token has to be an identifier, i.e., the name of
a procedure, a function, or a variable. (One other trivial possibility is
that this is an empty statement, if we're already up to the
semicolon, end, or until that marks the end of a statement.)
In any of these cases, the token we've just read is important to the parsing
procedure that will handle the simple statement, so statement un-reads
it before deciding what to do next. Gettype outputs the type of the
identifier, either a variable type like real or else procedure
or function. (The compiler data structures that underlie the work of
gettype will be discussed later.) If the token is a
procedure name, then this is a procedure call statement. If the token is a
function name, then this is the special kind of assignment inside a function
definition that provides the return value for the function. Otherwise, the
token must be a variable name and this is an ordinary assignment statement.
The procedure pif parses if statements. (The letter p in
its name stands for "Pascal"; many procedures in the compiler have such
names to avoid conflicts with Logo procedures with similar purposes.) The
syntax of Pascal if is
ifstatement: if boolean then statement |
if boolean then statement else statement
When pif begins, the token if has just been read by
statement. So the first thing that's required is a boolean expression.
Pexpr parses an expression; that task is relatively complicated and
will be discussed in more detail later. Pboolean ensures that the
expression just parsed does indeed produce a value of type boolean.
The next token in the source file must be the word then. The
instruction
mustbe "then
in pif ensures that. Here's mustbe:
to mustbe :wanted localmake "token token if equalp :token :wanted [stop] (throw "error (sentence "expected :wanted "got :token)) end
If mustbe returns successfully, pif then invokes
statement recursively to parse the true branch of the conditional.
The production rule tells us that there is then an optional false
branch, signaled by the reserved word else. The instruction
ifbe "else [statement]
handles that possibility. If the next token matches the first
input to ifbe then the second input, an instruction list, is carried
out. Otherwise the token is un-read. There is also an ifbeelse that
takes a third input, an instruction list to be carried out if the next token
isn't equal to the first input. (Ifbeelse still un-reads the token in
that case, before it runs the third input.) These must be macros so that
the instruction list inputs can include output or stop
instructions (as discussed in Volume 2), as in the invocations of ifbe
in statement seen a moment ago.
.macro ifbe :wanted :action localmake "token token if equalp :token :wanted [output :action] make "peektoken :token output [] end .macro ifbeelse :wanted :action :else localmake "token token if equalp :token :wanted [output :action] make "peektoken :token output :else end
If there were no code generation involved, pif would be written this
way:
to pif pboolean pexpr mustbe "then statement ifbe "else [statement] end
This simplified procedure is a straightforward translation of the RTN
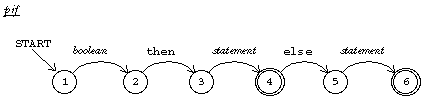
The need to generate object code complicates the parser. But don't let that distract you; in general you can see the formal structure of Pascal syntax reflected in the sequence of instructions used to parse that syntax.
The procedures that handle other structured statements, such as pfor
and pwhile, are a lot like pif. Procedure and function
declarations (procedures procedure, function, and proc1 in
the compiler) also use the same straightforward parsing technique, but are a
little more complicated because of the need to keep track of type
declarations for each procedure's parameters and local variables.
Ironically, the hardest thing to compile is the "simple" assignment
statement, partly because of operator precedence (multiplication before
addition) in expressions (procedure pexpr in the compiler) and partly
because of the need to deal with the complexity of variables, including
special cases such as assignments to var parameters and array elements.
I haven't yet showed you pboolean because you have to understand how
the compiler handles expressions first. But it's worth noticing that Pascal
can check at compile time whether or not an expression is going to
produce a boolean value even though the program hasn't been run yet
and the variables in the expression don't have values yet. It's the strict
variable typing of Pascal that makes this compile-time checking possible.
If we were writing a Logo compiler, the checking would have to be postponed
until run time because you can't, in general, know what type of datum will
be computed by a Logo expression until it's actually evaluated.
Arithmetic or boolean expressions appear not only on the right side of assignment statements but also as actual parameters, array index values, and as "phrases" in structured statements. One of the classic problems in compiler construction is the translation of these expressions to executable form. The interesting difficulty concerns operator precedence--the rule that in a string of alternating operators and operands, multiplications are done before additions, so
a + b * c + d
means
a + (b * c) + d
Pascal has four levels of operator precedence. The highest level, number 4,
is the unary operators +, -, and not. (The first
two can be used as unary operators (-3) or binary ones (
6-3); it's only in the unary case that they have this
precedence.)* Then comes multiplication, division, and
logical and at level 3. Level 2 has binary addition, subtraction, and
or. And level 1 includes the relational operators like
=.
*It's unfortunate that the word "binary" is used in
computer science both for base-2 numbers and for two-input operations.
Kenneth Iverson, in his documentation for the
language APL, used the words monadic and
dyadic instead of unary and binary to avoid that ambiguity. But
those terms haven't caught on.
The formalization of precedence could be done using the mechanisms we've already seen. For example, here is a production rule grammar for expressions using only the four basic arithmetic operations.
expression: term | expression + term | expression - term term: factor | term * factor | term / factor factor: variable | number | ( expression )
This grammar also introduces into the discussion the fact that the precedence of operations can be changed by using parentheses.
This grammar, although formally correct, is not so easy to use in a
recursive descent parser.
One subtle but important problem is that it's left recursive: Some
of the alternative forms for an expression start with an
expression. If we tried to translate this into a Logo procedure it would
naturally start out
to expression
local [left op right]
make "left expression
ifbe "+
[make "op "+
make "right term]
[ifbe "-
[make "op "-
make "right term]
[make "op []] ]
...
But this procedure will never get past the first make; it's
an infinite loop. It will never actually read a token from the source file;
instead it keeps invoking itself recursively.
Left association is a problem for automatic compiler compilers, too. There are ways to solve the problem but I don't want to get into that because in fact arithmetic expressions are generally handled by an entirely different scheme, which I'll show you in a moment. The problem wouldn't come up if the order of the operands were reversed, so the rules said
expression: term | term + expression | term - expression
and so on. Unfortunately this changes the meaning, and the rules of Pascal say that equal-precedence operations are performed left to right.
In any case, the formalization of precedence with production rules gets more complicated as the number of levels of precedence increases. I showed you a grammar with two levels. Pascal, with four levels, might reasonably be done in a similar way, but think about the C programming language, which has 15 levels of precedence!
What we're after is an algorithm that will allow the compiler to read an
expression once, left to right, and group operators and operands correctly.
The algorithm involves the use of two stacks, one for operations and one for
data. For each operation we need to know whether it's unary or binary and
what its precedence level is. I'll use the notation "*2,3" to
represent binary * at precedence level 3. So the expression
a + b * - c - d
will be represented in this algorithm as
 0 a +2,2 b *2,3 -1,4 c -2,2 d
0 a +2,2 b *2,3 -1,4 c -2,2 d 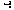 0
0
The symbols  and
and 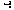 aren't really part of the source
expression; they're imaginary markers for the beginning and end of the
expression. When we read a token that doesn't make sense as part of an
expression, we can un-read that token and pretend we read a
aren't really part of the source
expression; they're imaginary markers for the beginning and end of the
expression. When we read a token that doesn't make sense as part of an
expression, we can un-read that token and pretend we read a 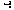 instead.
These markers are given precedence level zero because they form a boundary
for any operators inside them, just as a low-precedence operator like
instead.
These markers are given precedence level zero because they form a boundary
for any operators inside them, just as a low-precedence operator like
+ is a boundary for the operands of a higher-precedence operator like
*. (For the same reason, you'll see that parentheses are considered
precedence zero.)
The two minus signs in this expression have two different meanings. As you read the following algorithm description, you'll see how the algorithm knows whether an operation symbol is unary or binary.
Step 1. We initialize the two stacks this way:
operation: [0 ] data: [ ]
Step 2. We are now expecting a datum, such as a variable. Read a token. If it's an operation, it must be unary; subscript it accordingly and go to step 4. If it's a datum, push it onto the data stack. (If it's neither an operation nor a datum, something's wrong.)
Step 3. We are now expecting a binary operation. Read a token. If
it's an operation, subscript it as binary and go to step 4. If not, we've
reached the end of the expression. Un-read the token, and go to step 4 with
the token 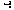 0.
0.
Step 4. We have an operation in hand at this point and we know its precedence level and how many arguments it needs. Compare its precedence level with that of the topmost (most recently pushed) operation on the stack. If the precedence of the new operation is less than or equal to that of the one on the stack, go to step 5. If it's greater, go to step 6.
Step 5. The topmost operation on the stack has higher precedence than
the one we just read, so we should do it right away. (For example, we've
just read the + in a*b+c; the multiplication operation and both
of its operands are ready on the stacks.) Pop the operation off
the stack, pop either one or two items off the data stack depending on the
first subscript of the popped operation, then compile machine instructions to
perform the indicated computation. Push the result on the data stack
as a single quantity. However, if the operation we popped is  , then
we're finished. There should be only one thing on the data stack, and it's
the completely compiled expression. Otherwise, we still have the new
operation waiting to be processed, so return to step 4.
, then
we're finished. There should be only one thing on the data stack, and it's
the completely compiled expression. Otherwise, we still have the new
operation waiting to be processed, so return to step 4.
Step 6. The topmost operation on the stack has lower precedence than
the one we just read, so we can't do it yet because we're still reading its
right operand. (For example, we've just read the * in a+b*c;
we're not ready to do either operation until we read the c later.)
Push the new operation onto the operation stack, then return to step 2.
Here's how this algorithm works out with the sample expression above. In
the data stack, a boxed entry like  means the result from
translating that subexpression into the object language.
means the result from
translating that subexpression into the object language.
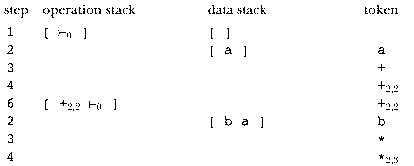

The final value on the data stack is the translation of the entire expression.
The algorithm so far does not deal with parentheses. They're handled
somewhat like operations, but with slightly different rules. A left
parenthesis is stored on the operation stack as (0, like the
special marker at the beginning of the expression, but it does not invoke
step 5 of the algorithm before being pushed on the stack. A right
parenthesis does invoke step 5, but only as far down the stack as
the first matching left parenthesis; if it were an ordinary operation of
precedence zero it would pop everything off the stack. You might try to
express precisely how to modify the algorithm to allow for parentheses.
Here are the procedures that embody this algorithm in the compiler.
Pgetunary and pgetbinary output a list like
[sub 2 2]
for binary - or
[minus 1 4]
for unary minus. (I'm leaving out some complications
having to do with type checking.) They work by looking for a unary or
binary property on the property list of the operation symbol.
Procedures with names like op.prec are selectors for the members
of these lists.
In this algorithm, only step 5 actually generates any instructions in the
object program. This is the step in which an operation is removed from
the operation stack and actually performed. Step 5 is carried out by the
procedure ppopop (Pascal pop operation); most of that procedure deals
with code generation, but I've omitted that part of the procedure in the
following listing because right now we're concerned with the parsing
algorithm. We'll return to code generation shortly.
Pexpr1 invokes pdata when it expects to read an operand, which
could be a number, a variable, or a function call. Pdata, which I'm
not showing here, generates code to make the operand available and
outputs the location of the result in the simulated computer, in a form
that can be used by pexpr.
to pexpr local [opstack datastack parenlevel] make "opstack [[popen 1 0]] ; step 1 make "datastack [] make "parenlevel 0 output pexpr1 end to pexpr1 local [token op] make "token token ; step 2 while [equalp :token "|(|] [popen make "token token] make "op pgetunary :token if not emptyp :op [output pexprop :op] push "datastack pdata :token make "token token ; step 3 while [and (:parenlevel > 0) (equalp :token "|)| )] [pclose make "token token] make "op pgetbinary :token if not emptyp :op [output pexprop :op] make "peektoken :token pclose if not emptyp :opstack [(throw "error [too many operators])] if not emptyp butfirst :datastack [(throw "error [too many operands])] output pop "datastack end to pexprop :op ; step 4 while [(op.prec :op) < (1 + op.prec first :opstack)] [ppopop] push "opstack :op ; step 6 output pexpr1 end to ppopop ; step 5 local [op function args left right type reg] make "op pop "opstack make "function op.instr :op if equalp :function "plus [stop] make "args op.nargs :op make "right pop "datastack make "left (ifelse equalp :args 2 [pop "datastack] [[[] []]]) make "type pnewtype :op exp.type :left exp.type :right ... code generation omitted ... push "datastack (list :type "register :reg) end to popen push "opstack [popen 1 0] make "parenlevel :parenlevel+1 end to pclose while [(op.prec first :opstack) > 0] [ppopop] ignore pop "opstack make "parenlevel :parenlevel - 1 end
We're ready to move from parsing to code generation, but first you must understand what a computer's native language is like. Most computer models in use today have a very similar structure, although there are differences in details. My simulated computer design makes these detail choices in favor of simplicity rather than efficiency. (It wouldn't be very efficient no matter what, compared to real computers. This "computer" is actually an interpreter, written in Logo, which is itself an interpreter. So we have two levels of interpretation involved in each simulated instruction, whereas on a real computer, each instruction is carried out directly by the hardware. Our compiled Pascal programs, as you've probably already noticed, run very slowly. That's not Pascal's fault, and it's not even primarily my compiler's fault, even though the compiler doesn't include optimization techniques. The main slowdown is in the interpretation of the machine instructions.)
Every computer includes a processor, which decodes instructions and carries out the indicated arithmetic operations, and a memory, in which information (such as the values of variables) is stored. In modern computers, the processor is generally a single integrated circuit, nicknamed a chip, which is a rectangular black plastic housing one or two inches on a side that contains thousands or even millions of tiny components made of silicon. The memory is usually a circuit board containing several memory chips. Computers also include circuitry to connect with input and output devices, but we're not going to have to think about those. What makes one computer model different from another is mainly the processor. If you have a PC, its processor is probably an Intel design with a name like 80486 or Pentium; if you have a Macintosh, the processor might be a Motorola 68040 or a Power PC chip.
It turns out that the wiring connecting the processor to the memory is often the main limiting factor on the speed of a computer. Things happen at great speed within the processor, and within the memory, but only one value at a time can travel from one to the other. Computer designers have invented several ways to get around this problem, but the important one for our purposes is that every modern processor includes a little bit of memory within the processor chip itself. By "a little bit" I mean that a typical processor has enough memory in it to hold 32 values, compared to several million values that can be stored in the computer's main memory. The 32 memory slots within the processor are called registers.*
*One current topic in computer architecture research
is the development of parallel computers with many processors working
together. In some of these designs, each processor includes its own
medium-size memory within the processor chip.
Whenever you want to perform an arithmetic operation, the operands must already be within the processor, in registers. So, for example, the Pascal instruction
c := a + b
isn't compiled into a single machine instruction. First we must
load the values of a and b from memory into registers,
then add the two registers, then store the result back into memory:
rload 8 a rload 9 b add 10 8 9 store 10 c
The first rload instruction loads the value from memory
location a into register 8.* The add instruction adds
the numbers in registers 8 and 9, putting the result into register 10. (In
practice, you'll see that the compiler would be more likely to conserve
registers by reusing one of the operand registers for the result, but for
this first example I wanted to keep things simple.) Finally we store the
result into the variable c in memory.
*Really I should have called this
instruction
load, but my machine simulator uses Logo procedures to
carry out the machine instructions, and I had to pick a name that wouldn't
conflict with the Logo load primitive.
The instructions above are actually not machine language instructions, but
rather assembly language instructions, a kind of shorthand.
A program called an assembler translates assembly language into
machine language, in which each instruction is represented as a number.
For example, if the instruction code for add is 0023, then
the add instruction above might be translated into 0023100809,
with four digits for the instruction code and two digits for each of the three
register numbers. (In reality the encoding would use binary numbers rather
than the decimal numbers I've shown in this example.) Since a machine
language instruction is just a number, the instructions that make up a
computer program are stored in memory along with the program's data values.
But one of the simplifications I've made in my simulated computer is that
the simulator deals directly with assembly language instructions, and those
instructions are stored in a Logo list, separate from the program's data memory.
The simulated computer has 32 processor registers plus 3000 locations of
main memory; it's a very small computer, but big enough for my sample
Pascal programs. (You can change these sizes by editing procedure
opsetup in the compiler.) The registers are numbered from 0 to 31, and
the memory locations are numbered from 0 to 2999. The number of a memory
location is called its address. Each memory location can hold
one numeric value.* A Pascal array will be represented by a contiguous block of
memory locations, one for each member of the array. Each register, too, can
hold one numeric value. In this machine, as in some real computers, register
number 0 is special; it always contains the value zero.
*This, too, is a simplification. In real computers,
different data types require different amounts of memory. A character
value, for example, fits into eight bits (binary digits) of memory,
whereas an integer requires 32 bits in most current computers. Instead of a
single
load instruction, a real computer has a separate one for each
datum size.
The simulated computer understands 50 instruction codes, fewer than most
real computers. The first group we'll consider are the 14 binary arithmetic
instructions: add, sub, mul, div (real quotient),
quo (integer quotient), rem (remainder), land (logical
and), lor (logical or), eql (compare two operands for equality),
neq (not equal), less, gtr (greater than), leq (less
than or equal), and geq (greater than or equal). The result of each
of the six comparison operators is 0 for false or 1 for true.
The machine also has four unary arithmetic instructions: lnot
(logical not), sint (truncate to integer), sround (round to
integer), and srandom. Each of these 18 arithmetic instructions takes
its operands from registers and puts its result into a register.
All but the last three of these are typical instructions of real
computers.*
(Not every computer has all of them; for example, if a computer has eql
and lnot, then it doesn't really need a neq instruction because
the same value can be computed by a sequence of two instructions.) The
operations sint, sround, and srandom are less likely to be
machine instructions on actual computers. On the other hand, most real
computers have a system call mechanism, which is a machine
instruction that switches the computer from the user's program to a part of
the operating system that performs some task on behalf of the user. System
calls are used mainly for input and output, but we can pretend that there are
system calls to compute these Pascal library functions. (The letter s
in the instruction names stands for "system call" to remind us.)
*One important simplification is that in the simulated
computer, the same instructions are used for all kinds of numbers. A typical
computer has three
add instructions: one for integers, one for short
reals (32 bits), and one for long reals (64 bits).
The simulated computer also has another set of 18 immediate
instructions, with the letter i added to the instruction name:
addi, subi, and so on. In these instructions, the rightmost operand
in the instruction is the actual value desired, rather than the number of
a register containing the operand. For example,
add 10 8 9
means, "add the number in register 8 and the number in register 9, putting the result into register 10." But
addi 10 8 9
means, "add the number in register 8 to the value 9, putting the result in register 10."
It's only the right operand that can be made immediate. So, for example, the Pascal assignment
y := x - 5
can be translated into
rload 8 x subi 8 8 5 store 8 y
but the Pascal assignment
y := 5 - x
must be translated as
addi 8 0 5 rload 9 x sub 8 8 9 store 8 y
This example illustrates one situation in which it's useful to have register 0 guaranteed to contain the value 0.
Our simulated machine has six more system call instructions having to do
with printing results. One of them, newline, uses no operands and
simply prints a newline character, moving to the beginning of a new line
on the screen. Four more are for printing the value in a register; the
instruction used depends on the data type of the value in the register.
The instructions are putch for a character, puttf for a boolean
(true or false) value, putint for an integer, and putreal for a
real number. Each takes two operands; the first, an immediate value, gives
the minimum width in which to print the value, and the second is a register
number. So the instruction
putint 10 8
means, "print the integer value in register 8, using at least
10 character positions on the line." The sixth printing instruction,
putstr, is used only for constant character strings in the Pascal
program; its first operand is a width, as for the others, but its second
is a Logo list containing the string to print:
putstr 1 [The shuffled deck:]
This is, of course, unrealistic; in a real computer the second operand would have to be the memory address of the beginning of the array of characters to print. But the way I handle printing isn't very realistic in any case; I wanted to do the simplest possible thing, because worrying about printing really doesn't add anything to your understanding of the process of compilation, which is the point of this chapter.
The next group of instructions has to do with the flow of control in the
computer program. Ordinarily the computer carries out its instructions
in sequence, that is, in the order in which they appear in the program.
But in order to implement conditionals (such as if), loops (such as
while), and procedure calls, we must be able to jump out of sequence.
The jump instruction takes a single operand, a label
that appears somewhere in the program. When the computer carries out a jump
instruction, it looks for the specified label and starts reading instructions
just after where that label appears in the program. (We saw an example of
labels at the beginning of this chapter.)
The jump instruction is used for unconditional jumps. In order to
implement conditionals and loops, we need a way to jump if some condition
is true. The instruction jumpt (jump if true) has two operands,
a register number and a label. It jumps to the specified label if and only
if the given register contains a true value. (Since registers hold only
numbers, we use the value 1 to represent true, and 0 to represent false.)
Similarly, jumpf jumps if the value in the given register is false.
For procedure and function calls, we need a different mechanism. The jump
is unconditional, but the computer must remember where it came from, so that
it can continue where it left off once the called procedure or function
returns. The instruction jal (jump and link) takes two operands, a
register and a label. It puts into the register the address of the
instruction following the jal instruction.* Then it jumps to the specified label.
To return from the called procedure, we use the jr (jump register)
instruction. It has one operand, a register number; it jumps to the
instruction whose address is in the register.
*In a real computer,
each instruction is stored in a particular memory location, so the address
of an instruction is the address of the memory location in which it's stored.
In this simulated computer, I keep the program in the form of a Logo list,
and so I cheat and put the sublist starting at the next instruction into
the register. This isn't quite as much of a cheat as it may seem, though,
since you know from Chapter 3 that Logo represents a list with the memory
address of the first pair of the list.
One final instruction that affects the flow of control is the exit
system call. It requires no operands; it terminates the running of the
program. In this simulated computer, it returns to a Logo prompt; in a
real computer, the operating system would start running another user program.
The only remaining instructions are rload and store. You already
know what these do, but I've been showing them in oversimplified form so far.
The second operand can't just be a variable name, because that variable might
not be in the same place in memory every time the procedure is called. Think,
for example, about a recursive procedure. Several invocations may be in
progress at once, all of them carrying out the same compiled instructions,
but each referring to a separate set of local variables. The solution to
this problem is that the compiler arranges to load into a register
the address of a block of memory containing all the local variables for a
given procedure call. If the variable c, for example, is in the sixth
memory location of that block, an instruction to load or store that variable
must be able to say "the memory location whose address is the contents of
register 4 (let's say) plus five." So each load and store instruction
contains an index register in parentheses following an
offset to be added to the contents of that register. We'd say
store 8 5(4)
to store the contents of register 8 into the variable c,
provided that register 4 points to the correct procedure invocation's
local variables and that c is in the sixth position in the block.
(The first position in the block would have offset 0, and so on.)
The first step in invoking a procedure or function is to set aside, or allocate, a block of memory locations for use by that invocation. This block will include the procedure's local variables, its arguments, and room to save the values of registers as needed. The compiler's data structures include, for each procedure, how much memory that procedure needs when it's invoked. That block of memory is called a frame.
In most programming languages, including Pascal and Logo (but not, as it turns out, Lisp), the frame allocated when a procedure invocation begins can be released, or deallocated, when that invocation returns to its caller. In other words, the procedure's local variables no longer exist once the invocation is finished. In these languages, the frames for all the active procedure invocations can be viewed as a stack, a data structure to which new elements are added by a Push operation, and elements are removed using a Pop operation that removes the most recently pushed element. (In this case, the elements are the frames.) That is, suppose that procedure A invokes B, which invokes C, which invokes D. For each of these invocations a new frame is pushed onto the stack. Which procedure finishes first? It has to be D, the last one invoked. When D returns, its frame can be popped off the stack. Procedure C returns next, and its frame is popped, and so on. The phrase stack frame is used to refer to frames that behave like elements of a stack.
My Pascal compiler allocates memory starting at location 0 and working upward. At the beginning of the program, a global frame is allocated to hold the program's global variables. Register 3, the global pointer, always contains the address of the beginning of the global frame, so that every procedure can easily make use of global variables. (Since the global frame is the first thing in memory, its address is always zero, so the value in register 3 is always 0. But in a more realistic implementation the program itself would appear in memory before the global frame, so its address would be greater than zero.)
At any point in the program, register 4, the frame pointer, contains the address of the beginning of the current frame, that is, the frame that was created for the current procedure invocation. Register 2, the stack pointer, contains the address of the first currently unused location in memory.
My compiler is a little unusual in that when a procedure is called, the
stack frame for the new invocation is allocated by the caller, not by the
called procedure. This simplifies things because the procedure's arguments
can be stored in its own frame; if each procedure allocates its own frame,
then the caller must store argument values in its (the caller's) frame,
because the callee's frame doesn't exist yet. So, in my compiler, the
first step in a procedure call is to set register 5, the new frame
pointer, to point to the first free memory location, and change the
stack pointer to allocate the needed space. If N memory locations
are needed for the new frame, the calling procedure will contain the
following instructions:
add 5 2 0 addi 2 2 N
The first instruction copies the value from register 2 (the
first free memory location) into register 5; the second adds N to
register 2. (I've left out a complication, which is that the old value
in register 5 must be saved somewhere before putting this new value
into it. You can read the code generation instructions at the beginning
of pproccall1, in the program listing at the end of the chapter,
for all the details.) The current frame pointer is also saved in
location 3 of the new frame:
store 4 3(5)
The compiler uses data abstraction to refer to these register
numbers and frame slots; for example, the procedure reg.frameptr takes
no arguments and always outputs 4, while frame.prevframe outputs 3.
The next step is to put the argument values into the new frame. During this process, the calling procedure must use register 4 to refer to its own variables, and register 5 to refer to the callee's variables. The final step, just before calling the procedure, is to make the frame pointer (register 4) point to the new frame:
add 4 5 0
Once the caller has set up the new frame and saved the necessary registers, it can call the desired procedure, putting the return address in register 1:
jal 1 "proclabel
The first step in the called procedure is to save the return address in location zero of its frame:
store 1 0(4)
The procedure then carries out the instructions in its body. When it's ready to return, it must load the saved return address back into register 1, then restore the old stack pointer and frame pointer to deallocate its frame, and finally return to the caller:
rload 1 0(4) add 2 4 0 rload 4 3(2) jr 1
(Procedure proc1 in the compiler generates these
instructions for each procedure.)
One final complication about stack frames comes from Pascal's block structure. Suppose we have a program with internal procedures arranged in this structure:
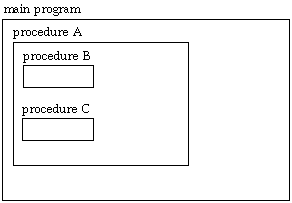
Then suppose that the main program calls procedure A, which calls B, which calls C, which calls itself recursively. The current (inner) invocation of C has access to its own variables, those of procedure A, and the global variables, but not to procedure B's variables. How does procedure C know where procedure A's stack frame is located? The answer is that every frame, in addition to saving a pointer to the previous frame, must include a pointer to the lexically enclosing frame. The calling procedure sets this up; it can do this because it knows its own lexical depth and that of the called procedure. For example, when procedure B calls procedure C, C's lexically enclosing frame will be the same as B's (namely, the frame for the invocation of A), because B and C are at the same lexical depth. (They are both declared inside A.) But when procedure A calls procedure B, which is declared within itself, A must store its own frame pointer as B's lexically enclosing frame. Here is a picture of what's where in memory:
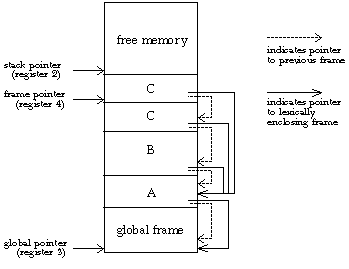
If all these pointers between frames confuse you, it might help to keep in mind that the two kinds of pointers have very different purposes. The pointer to the previous frame is used only when a procedure returns, to help in putting everything back the way it was before the procedure was called (in particular, restoring the old value of register 4). The pointer to the lexically enclosing frame is used while the procedure is running, whenever the procedure makes reference to a variable that belongs to some outer procedure (for example, a reference in procedure B or C to a variable that belongs to procedure A).*
*If procedures used the previous-frame
pointers to make variable references, we would be compiling a dynamically
scoped language! In this example, because Pascal is lexically scoped,
procedure C can't refer to procedure B's variables, even though B called C.
In this section I'll describe the main data structures used during compilation (abstract data types for identifiers and for expressions) and during the running of the program (registers and frames).
The main body of information that the compiler must maintain is the list of
Pascal identifiers (variable, procedure, and function names). Since Pascal
is lexically scoped, some attention is necessary to ensure that each compiled
Pascal procedure has access to precisely the variables that it should.
At any point during the compilation, the value of :idlist is a list of
just those identifiers that may be used in the part of the program being
compiled. We'll see in a moment how that's accomplished.
There are two main categories of identifier: procedure names (including the main program and functions in this category) and variable names. The information maintained for a procedure name looks like this example:
[myproc procedure %myproc [2 46]]
The first member of this list is the Pascal name of the program,
procedure, or function. The second member is the type indicator, which
will be one of the words program, procedure, or function.
The third member is the procedure's "Logo name," the unique name used within
the compiler to represent this program or procedure. The program's Logo name
is used as the variable name whose value will be the compiled program; the
Logo names for procedures and functions are used as the labels in the
compiled program at which each procedure or function begins. The fourth
member of the list contains the frame information for the procedure; it's
a list of two numbers, the lexical depth and the frame size. The lexical
depth is 0 for the main program, 1 for a procedure declared inside the
main program, 2 for a procedure declared inside a depth-1 procedure, and
so on. The frame size indicates how many memory locations must be allocated
for each invocation of the procedure. (For the main program, the frame size
indicates the size of the global frame.)
Because of the Pascal scope rules, there can be two procedures with the same
name, each declared within a different region of the program. But there is
no scoping of labels in the compiled program; each label must be unique.
The simplest solution would be to use a distinct program-generated name for
every Pascal procedure; the Pascal doit would become the
Logo g14. In fact I chose to modify this approach somewhat. When an
identifier symbol is declared in the source program, the compiler
looks to see whether another identifier with the same name has appeared
anywhere in the program. If not, the Logo name %symbol is used; if
so, a generated symbol is used. This rule makes the compiled
program a little easier to read, while preserving the rule that all Logo
names must be unique. The percent sign in %symbol ensures that this
Logo name doesn't conflict with any names used in the
compiler itself. Procedure newlname in the compiler takes a Pascal
identifier as input and generates a new Logo name to correspond.
The selectors id.type, id.lname, and id.frame are used
for the second through fourth members of these lists. There's no selector
for the first member, the Pascal name, because the compiler never
extracts this information explicitly. Instead, the Pascal name is used
by procedure getid, which takes a Pascal name as its input and
returns the corresponding identifier list.
For variable names, the identifier information looks a little different:
[i integer [1 41] false]
The first two members of this list are the Pascal name and the
type, the same as for a procedure. The third member is the pointer
information for the variable: its lexical depth and the offset within
a frame where it should be kept. The compiler will use this information
to issue instructions to load or store the value of the variable. The
fourth member of the list is true if this variable is a var
(call by reference) parameter, false otherwise.
The variable i above has a scalar type, so its type indicator is
a word. Had it been an array, the type indicator would be a list such as
[integer [0 6] [5 3]]
for a variable declared as array [0..5, 5..7] of integer.
For each dimension of the array, the first number in the list
is the smallest possible index, while the second number is the number of
possible index values in this dimension. That is, the range [3..7]
is represented by the list [3 5] because there are five possible
values starting from 3. Notice that there is no "Logo name" for a
variable; in the compiled program, a variable is represented as an
offset and an index register, such as 41(4).
For variables, the selectors used are id.type, id.pointer,
and id.varp.
The information about currently accessible identifiers is kept in the list
idlist. This variable holds a list of lists; each Pascal identifier
is represented by a list as indicated above. Idlist is a local
variable in the compiler procedures program, procedure, and
function. That is, there is a separate version for each block of the
Pascal source program. Each local version starts out with the same value as
the higher-level version; identifiers declared within a block are added to
the local version but not to the outer one. When the compiler finishes a
block, the (Logo) procedure in charge of that block stops and the outer
idlist becomes current again.
This arrangement may or may not seem strange to you. Recall that we had to
invent this idlist mechanism because Pascal's
lexical scope is different from Logo's dynamic scope. The reason we have
these different versions of idlist is to keep track of which
identifiers are lexically available to which blocks. And yet we are using
Logo's dynamic scope to determine which idlist is available at any
point in the compilation. The reason this works is that the
dynamic environment at compile time reflects the
lexical environment at run time. For example, in the tower
program, the fact that tower contains hanoi, which in
turn contains movedisk, is reflected in the fact that program
(compiling tower) invokes procedure (compiling
hanoi), which in turn invokes procedure recursively
(compiling movedisk). Earlier I said that lexical scope is easier for
a compiler than dynamic scope; this paragraph may help you see why that's
true. Even dynamically scoped Logo naturally falls into providing lexical
scope for a Pascal compiler.
Here is how procedure and function declarations are compiled:
to procedure proc1 "procedure framesize.proc end to function proc1 "function framesize.fun end to proc1 :proctype :framesize localmake "procname token localmake "lexical.depth :lexical.depth+1 localmake "frame (list :lexical.depth 0) push "idlist (list :procname :proctype (newlname :procname) :frame) localmake "idlist :idlist ... end
(I'm leaving out the code generation part for now.) What I want
to be sure you understand is that the push instruction adds the new
procedure name to the outer idlist; after that, it creates a
new idlist whose initial value is the same as the old one. It's very
important that the instruction
localmake "idlist :idlist
comes where it does and not at the beginning of the procedure.
Proc1 needs access to the outer idlist when it starts, and
then later it "shadows" that variable with its own local version. This
example shows that Logo's local command really is an executable
command and not a declaration like Pascal's var declaration. In
Pascal it would be unthinkable to declare a new local variable in the middle
of a block.
Getid depends on Logo's dynamic scope to give it access to the right
version of idlist. Think about writing a Pascal compiler in Pascal.
There would be a large block for program with many other procedures
inside it. Two of those inner procedures would be the ones for
procedure and function. (Of course they couldn't have those names,
because they're Pascal reserved words. They'd be called
compileprocedure or some such thing. But I think this will be easier to
follow if I stick with the names used in the Logo version of the compiler.)
Those two procedures should be at the same level of block structure; neither
should be lexically within the other. That's because a Pascal procedure
block can include a function definition or vice versa. Now, where in the
lexical structure does getid belong? It needs access to the local
idlist of either procedure or function, whichever is
currently active. Similarly, things like statement need to be
lexically within both procedure and function, and actually also
within program because the outermost program block has statements too.
It would theoretically be possible to solve the problem by writing three
identical versions of each of these subprocedures, but that solution is too
horrible to contemplate. Instead a more common technique is to have only
one idlist variable, a global one, and write the compiler so that it
explicitly maintains a stack of old values of that variable. The Pascal
programmer has to do the work that the programming language should be doing
automatically. This is an example in which dynamic scope, while not
absolutely essential, makes the program much easier to write and more
straightforward to understand.
For every procedure or function in the Pascal source program, the compiler creates a global Logo variable with the same name as the corresponding label--that is, either a percent-prefix name or a generated symbol. The value of this variable is a list of types, one for each argument to the procedure or function. (For a function, the first member of the list is the type of the function itself; the butfirst is the list of types of its arguments.) The compiler examines this "type signature" variable when a procedure or function is invoked, to make sure that the types of the actual arguments match the types of the formal parameters.
The other important compile-time data structure is the one that represents
a compiled expression. When the compiler calls pexpr, its job is to
parse an expression from the Pascal source program and generate code to
compute (when the compiled program runs!) the value of the expression.
The generated code leaves the computed value in some register. What
pexpr returns to its caller is a data structure indicating which register
and what type the expression has, like this:
[real register 8]
The first member of this list is the type of the expression.
Most of the time, the second member is the word register and the
third member is the register number in which the expression's value
can be found. The only exception is for a constant expression; if
the expression is, for example, 15 then pexpr will output
[integer immediate 15]
For the most part, these immediate expressions are useful
only within recursive calls to pexpr. In compiling the Pascal
assignment
x := 15
we're going to have to get the value 15 into a register anyway
in order to be able to store it into x; the generated code will be
something like
addi 7 0 15 store 7 48(4)
An immediate expression is most useful in compiling something like
x := a+15
in which we can avoid loading the value 15 into a register, but
can directly add it to the register containing a:
rload 7 53(4) addi 7 7 15 store 7 48(4)
The members of an expression list are examined using the selectors
exp.type, exp.mode (the word register or immediate),
and exp.value (the register number or immediate value).
In this compiler an "expression" is always a
scalar type; although the formal definition of Pascal allows for
array expressions, there are no operations that act on arrays the way
operations like + act on scalars, and so an array expression can only
be the name of an array variable. (Members of arrays can, of
course, be part of a scalar expression.) Passign, the compiler
procedure that handles assignment statements, first checks for the special
case of an array assignment and then, only if the left side of the
assignment is a scalar, invokes pexpr to parse a scalar expression.
In order to understand the code generated by the compiler, you should also know about the runtime data structures used by compiled programs. First, certain registers are reserved for special purposes:
| number | name | purpose | ||
|---|---|---|---|---|
| 0 | reg.zero | always contains zero | ||
| 1 | reg.retaddr | return address from procedure call | ||
| 2 | reg.stackptr | first free memory address | ||
| 3 | reg.globalptr | address of global frame | ||
| 4 | reg.frameptr | address of current frame | ||
| 5 | reg.newfp | address of frame being made for procedure call | ||
| 6 | reg.retval | return value from function | ||
| 7 | reg.firstfree | first register available for expressions |
We've already seen most of these while discussing stack frames. A Pascal function returns its result in register 6; the caller immediately copies the return value into some other register so that it won't be lost if the program calls another function, for a case like
x := f(3)+f(4)
Whenever a register is needed to hold some computed value, the compiler
calls the Logo procedure newregister, which finds the first register
number starting from 7 that isn't currently in use. When the value in
a register is no longer needed, the compiler calls regfree to indicate
that that register can be reassigned by newregister.
The other noteworthy runtime data structure is the use of slots within each frame for special purposes:
| number | name | purpose | ||
|---|---|---|---|---|
| 0 | frame.retaddr | address from which this procedure was called | ||
| 1 | frame.save.newfp | saved register 3 while filling this new frame | ||
| 2 | frame.outerframe | the frame lexically enclosing this one | ||
| 3 | frame.prevframe | the frame from which this one was called | ||
| 4-35 | frame.regsave | space for saving registers | ||
| 36 | frame.retval | function return value |
Why is there both a register and a frame slot for a function's return value? Remember that the way you indicate the return value in a Pascal function is by assigning to the function's name as if it were a variable. Such an assignment is not necessarily the last instruction in the function; it may do more work after computing the return value. The compiler notices as assignment to the function name and generates code to save the computed value in slot 36 of the current frame. Then, when the function actually returns, the compiler generates the instruction
rload 6 36(4)
to copy the return value into register 6. The function's frame is about to be freed, so the caller can't look there for the return value; that's why a register is used.
Each frame includes a block of space for saving registers when another procedure is called. That's because each procedure allocates register numbers independently; each starts with register 7 as the first free one. So if the registers weren't saved before a procedure call and restored after the call, the values in the registers would be lost. (Although the frame has enough room to save all 32 registers, to make things simple, not all 32 are actually saved. The compiler knows which registers contain active expression values at the moment of the procedure call, and it generates code to save and restore only the necessary ones.)
You might think it would be easier to have each procedure use a separate set of registers, so saving wouldn't be necessary. But this doesn't work for two reasons. First, there are only a few registers, and in a large program we'd run out. Even more important, the compiled code for a recursive procedure is going to use the same registers in each invocation, so we certainly can't avoid saving registers in that situation.
Let's look again at how the compiler handles a Pascal if statement:
to pif local [cond elsetag endtag] make "cond pboolean pexpr make "elsetag gensym make "endtag gensym mustbe "then code (list "jumpf :cond (word "" :elsetag)) regfree :cond statement code (list "jump (word "" :endtag)) code :elsetag ifbe "else [statement] code :endtag end
I showed you this procedure while talking about parsing, asking you to ignore the parts about code generation. Now we'll come back to that part of the process.
The format of the if statement is either of these:
if condition then statement if condition then statement else statement
(There is probably a semicolon after the statement, but it's
not officially part of the if; it's part of the compound statement
that contains the if.) When we get to pif, the compiler has
already read the token if; the next thing to read is an expression,
which must be of type boolean, providing the condition part of the
statement.
In the instruction
make "cond pboolean pexpr
the call to pexpr generates code for the expression and
returns an expression list, in the format shown earlier. The procedure
pboolean does three things: First, it checks the mode of the expression;
if it's immediate, the value is loaded into a register. Second, it checks
the type of the expression to ensure that it really is boolean. Third,
pboolean returns just the register number, which will be used in code
generated by pif.
to pboolean :expr [:pval noimmediate :expr]
if equalp exp.type :pval "boolean [output exp.value :pval]
(throw "error sentence exp.type :pval [not true or false])
end
to noimmediate :value
if equalp exp.mode :value "immediate ~
[localmake "reg newregister
code (list "addi :reg reg.zero exp.value :value)
output (list exp.type :value "register :reg)]
output :value
end
Overall, the code compiled for the if statement will look like this:
... get condition into register cond ...
jumpf cond "g5
... code for then statement ...
jump "g6
g5
... code for else statement ...
g6
The labels g5 and g6 in this example are generated
symbols; they'll be different each time. The labels are generated by the
instructions
make "elsetag gensym make "endtag gensym
in pif. After we call pexpr to generate the code
for the conditional expression, we explicitly generate the jumpf
instruction:
code (list "jumpf :cond (word "" :elsetag)) regfree :cond
Notice that once we've generated the jumpf instruction, we
no longer need the value in register :cond, and we call regfree
to say so. The rest of this code generation process should be easy to work
out. All of the structured statements (for, while, and
repeat) are similarly simple.
The code generation for expressions is all in ppopop. Most of the
complexity of dealing with expressions is in the parsing, not in the code
generation; by the time we get to ppopop, we know that we want to
carry out a single operation on two values, both of which are either in
registers or immediate values. The simple case is that both are in
registers; suppose, for example, that we are given the subtraction operation
and the two operands are in registers 8 and 9. Then we just generate the
instruction
sub 8 8 9
and declare register 9 free. Ppopop is a little long,
because it has to check for special cases such as immediate operands.
Also, a unary minus is turned into a subtraction from register zero,
since there is no unary minus operation in our simulated machine.
Ironically, it's the "simple" statements that are hardest to
compile: assignment and procedure calling. For procedure (or function)
calling, the difficulty is in matching actual argument expressions with
formal parameters. Procedure pproccall1 generates the instructions to
manipulate frame pointers, as described earlier, and procedure
procargs fills the newly-created frame with the actual argument values.
(If an argument is an array passed by value, each member of the array must
be copied into the new frame.) Assignment, handled by procedure
passign in the compiler, is similar to argument passing; a value must be
computed and then stored into a frame. I wouldn't be too upset if you
decide to stop here and take code generation for memory references on faith.
Suppose we are compiling the assignment
x := expression
Passign reads the name x and uses getid to find
the information associated with that name. If the assignment is to an array
member, then passign must also read the array indices, but let's say
that we are assigning to a scalar variable, to keep it simple.
to passign local [name id type index value pointer target] make "name token make "index [] ifbe "|[| [make "index commalist [pexpr] mustbe "|]|] mustbe "|:=| make "id getid :name make "pointer id.pointer :id make "type id.type :id passign1 end
Procedure passign1 contains the steps that are in common between
ordinary assignment (handled by passign) and assignment to the name of
the current function, to set the return value (handled by pfunset,
which you can read in the complete listing at the end of the chapter).
to passign1 if and (listp :type) (emptyp :index) [parrayassign :id stop] setindex "false make "value check.type :type pexpr codestore :value (id.pointer :id) (id.varp :id) :index regfree :value end
We call pexpr to generate the code to compute the
expression. Check.type is like pboolean, which you saw earlier,
except that it takes the desired type as an argument. It returns the
number of the register that contains the expression value.
The real work is done by codestore, which takes four inputs.
The first is the register number whose value should be stored; the other
three inputs indicate where in memory the value should go. First comes the
pointer from the identifier list; this, you'll recall, tells us the lexical
depth at which the variable was declared and the offset within its frame
where the variable is kept. Next is a true or false value indicating
whether or not this variable is a var parameter; if so, then its value
is a pointer to the variable whose value we really want to change.
Finally, the index input will be zero for a scalar variable, or the
number of a register containing the
array index for an array member. (Procedure lindex, whose name stands
for "linear index," has been called to generate code to convert the possible
multi-dimensional indices, with possibly varying starting values, into a
single number indicating the position within the array, starting from zero
for the first member.)
to codestore :reg :pointer :varflag :index localmake "target memsetup :pointer :varflag :index code (list "store :reg targetaddr) regfree last :target end
(There is a similar procedure codeload used to generate
the code to load a variable's value into a register.) Codestore
invokes a subprocedure memsetup whose job is to work out an
appropriate operand for an rload or store machine instruction.
That operand must be an offset and an index register, such as 41(4).
What memsetup returns is a list of the two numbers, in this case
[41 4]. Procedure targetaddr turns that into the right notation
for use in the instruction.
Memsetup is the most complicated procedure in the compiler, because
there are so many special cases. I'll describe the easy cases here. Suppose
that we are dealing with a scalar variable that isn't a var parameter.
Then there are three cases. If the lexical depth of that variable is equal
to the current lexical depth, then this variable is declared in the same
block that we're compiling. In that case, we use register 4 (the current
frame pointer) as the index register, and the variable's frame slot as the
offset. If the variable's lexical depth is zero, then it's a global
variable. In that case, we use register 3 (the global frame pointer) as
the index register, and the variable's frame slot as the offset. If the
variable's depth is something other than zero or the current depth, then
we have to find a pointer to the variable's own frame by looking in the
current frame's frame.outerframe slot, and perhaps in that
frame's frame.outerframe slot, as many times as the difference between
the current depth and the variable's depth.
If the variable is a var parameter, then we go through the same cases
just described, and then load the value of that variable (which is a pointer
to the variable we really want) into a register. We use that new register
as the index register, and zero as the offset.
If the variable is an array member, then we must add the linear index (which is already in a register) to the offset as computed so far.
Perhaps an example will help sort this out. Here is the compiled version
of the tower program, with annotations:
[ [add 3 0 0] set up initial pointers
[add 4 0 0]
[addi 2 0 36]
[jump "g1] jump to main program
%hanoi [store 1 0(4)] save return value
[jump "g2] jump to body of hanoi
%movedisk [store 1 0(4)]
[jump "g3]
g3 [putstr 1 [Move disk ]] body of movedisk
[rload 7 36(4)]
[putint 1 7] write(number:1)
[putstr 1 [ from ]]
[rload 7 37(4)]
[putch 1 7] write(from:1)
[putstr 1 [ to ]]
[rload 7 38(4)]
[putch 1 7] write(to:1)
[newline]
[rload 1 0(4)] reload return address
[add 2 4 0] free stack frame
[rload 4 3(2)]
[jr 1] return to caller
g2 [rload 7 36(4)] body of hanoi
[neqi 7 7 0] if number <> 0
[jumpf 7 "g4]
[store 5 1(2)] allocate new frame
[add 5 2 0]
[addi 2 2 40]
[store 4 3(5)] set previous frame
[rload 7 2(4)]
[store 7 2(5)] set enclosing frame
[rload 7 36(4)]
[subi 7 7 1]
[store 7 36(5)] first arg is number-1
[rload 7 37(4)]
[store 7 37(5)] next arg is from
[rload 7 39(4)]
[store 7 38(5)] next arg is other
[rload 7 38(4)]
[store 7 39(5)] next arg is onto
[add 4 5 0] switch to new frame
[rload 5 1(4)]
[jal 1 "%hanoi] recursive call
[store 5 1(2)] set up for movedisk
[add 5 2 0]
[addi 2 2 39]
[store 4 3(5)]
[store 4 2(5)] note different enclosing frame
[rload 7 36(4)]
[store 7 36(5)] copy args
[rload 7 37(4)]
[store 7 37(5)]
[rload 7 38(4)]
[store 7 38(5)]
[add 4 5 0]
[rload 5 1(4)]
[jal 1 "%movedisk] call movedisk
[store 5 1(2)] second recursive call
[add 5 2 0]
[addi 2 2 40]
[store 4 3(5)]
[rload 7 2(4)]
[store 7 2(5)]
[rload 7 36(4)]
[subi 7 7 1]
[store 7 36(5)]
[rload 7 39(4)]
[store 7 37(5)]
[rload 7 38(4)]
[store 7 38(5)]
[rload 7 37(4)]
[store 7 39(5)]
[add 4 5 0]
[rload 5 1(4)]
[jal 1 "%hanoi]
[jump "g5] end of if...then
g4
g5 [rload 1 0(4)] return to caller
[add 2 4 0]
[rload 4 3(2)]
[jr 1]
g1 [store 5 1(2)] body of main program
[add 5 2 0] prepare to call hanoi
[addi 2 2 40]
[store 4 3(5)]
[store 4 2(5)]
[addi 7 0 5] constant argument 5
[store 7 36(5)]
[addi 7 0 97] ASCII code for 'a'
[store 7 37(5)]
[addi 7 0 98] ASCII code for 'b'
[store 7 38(5)]
[addi 7 0 99] ASCII code for 'c'
[store 7 39(5)]
[add 4 5 0]
[rload 5 1(4)]
[jal 1 "%hanoi] call hanoi
[exit]
]
| (back to Table of Contents) | BACK chapter thread NEXT |
to compile :file
if namep "peekchar [ern "peekchar]
if namep "peektoken [ern "peektoken]
if not namep "idlist [opsetup]
if not emptyp :file [openread :file]
setread :file
ignore error
catch "error [program]
localmake "error error
if not emptyp :error [print first butfirst :error]
setread []
if not emptyp :file [close :file]
end
;; Global setup
to opsetup
make "numregs 32
make "memsize 3000
pprop "|=| "binary [eql 2 [boolean []] 1]
pprop "|<>| "binary [neq 2 [boolean []] 1]
pprop "|<| "binary [less 2 [boolean []] 1]
pprop "|>| "binary [gtr 2 [boolean []] 1]
pprop "|<=| "binary [leq 2 [boolean []] 1]
pprop "|>=| "binary [geq 2 [boolean []] 1]
pprop "|+| "binary [add 2 [[] []] 2]
pprop "|-| "binary [sub 2 [[] []] 2]
pprop "or "binary [lor 2 [boolean boolean] 2]
pprop "|*| "binary [mul 2 [[] []] 3]
pprop "|/| "binary [quo 2 [real []] 3]
pprop "div "binary [div 2 [integer integer] 3]
pprop "mod "binary [rem 2 [integer integer] 3]
pprop "and "binary [land 2 [boolean boolean] 3]
pprop "|+| "unary [plus 1 [[] []] 4]
pprop "|-| "unary [minus 1 [[] []] 4]
pprop "not "unary [lnot 1 [boolean boolean] 4]
make "idlist `[[trunc function int [1 ,[framesize.fun+1]]]
[round function round [1 ,[framesize.fun+1]]]
[random function random [1 ,[framesize.fun+1]]]]
make "int [integer real]
make "round [integer real]
make "random [integer integer]
end
;; Block structure
to program
mustbe "program
localmake "progname token
ifbe "|(| [ignore commalist [id] mustbe "|)|]
mustbe "|;|
localmake "lexical.depth 0
localmake "namesused []
localmake "needint "false
localmake "needround "false
localmake "needrandom "false
localmake "idlist :idlist
localmake "frame [0 0]
localmake "id (list :progname "program (newlname :progname) :frame)
push "idlist :id
localmake "codeinto word "% :progname
make :codeinto []
localmake "framesize framesize.proc
program1
mustbe ".
code [exit]
foreach [int round random] "plibrary
make :codeinto reverse thing :codeinto
end
to program1
localmake "regsused (array :numregs 0)
for [i reg.firstfree :numregs-1] [setitem :i :regsused "false]
ifbe "var [varpart]
.setfirst butfirst :frame :framesize
if :lexical.depth = 0 [code (list "add reg.globalptr reg.zero reg.zero)
code (list "add reg.frameptr reg.zero reg.zero)
code (list "addi reg.stackptr reg.zero :framesize)]
localmake "bodytag gensym
code (list "jump (word "" :bodytag))
tryprocpart
code :bodytag
mustbe "begin
blockbody "end
end
to plibrary :func
if not thing (word "need :func) [stop]
code :func
code (list "rload reg.firstfree (memaddr framesize.fun reg.frameptr))
code (list (word "s :func) reg.retval reg.firstfree)
code (list "add reg.stackptr reg.frameptr reg.zero)
code (list "rload reg.frameptr (memaddr frame.prevframe reg.stackptr))
code (list "jr reg.retaddr)
end
;; Variable declarations
to varpart
local [token namelist type]
make "token token
make "peektoken :token
if reservedp :token [stop]
vargroup
foreach :namelist [newvar ? :type]
mustbe "|;|
varpart
end
to vargroup
make "namelist commalist [id]
mustbe ":
ifbe "packed []
make "type token
ifelse equalp :type "array [make "type arraytype] [typecheck :type]
end
to id
local "token
make "token token
if letterp ascii first :token [output :token]
make "peektoken :token
output []
end
to arraytype
local [ranges type]
mustbe "|[|
make "ranges commalist [range]
mustbe "|]|
mustbe "of
make "type token
typecheck :type
output list :type :ranges
end
to range
local [first last]
make "first range1
mustbe "..
make "last range1
if :first > :last ~
[(throw "error (sentence [array bounds not increasing:]
:first ".. :last))]
output list :first (1 + :last - :first)
end
to range1
local "bound
make "bound token
if equalp first :bound "' [output ascii first butfirst :bound]
if equalp :bound "|-| [make "bound minus token]
if equalp :bound int :bound [output :bound]
(throw "error sentence [array bound not ordinal:] :bound)
end
to typecheck :type
if memberp :type [real integer char boolean] [stop]
(throw "error sentence [undefined type] :type)
end
to newvar :pname :type
if reservedp :pname [(throw "error sentence :pname [reserved word])]
push "idlist (list :pname :type (list :lexical.depth :framesize) "false)
make "framesize :framesize + ifelse listp :type [arraysize :type] [1]
end
to arraysize :type
output reduce "product map [last ?] last :type
end
;; Procedure and function declarations
to tryprocpart
ifbeelse "procedure ~
[procedure tryprocpart] ~
[ifbe "function [function tryprocpart]]
end
to procedure
proc1 "procedure framesize.proc
end
to function
proc1 "function framesize.fun
end
to proc1 :proctype :framesize
localmake "procname token
localmake "lexical.depth :lexical.depth+1
localmake "frame (list :lexical.depth 0)
push "idlist (list :procname :proctype (newlname :procname) :frame)
localmake "idlist :idlist
make lname :procname []
ifbe "|(| [arglist]
if equalp :proctype "function ~
[mustbe ":
localmake "type token
typecheck :type
make lname :procname fput :type thing lname :procname]
mustbe "|;|
code lname :procname
code (list "store reg.retaddr (memaddr frame.retaddr reg.frameptr))
program1
if equalp :proctype "function ~
[code (list "rload reg.retval (memaddr frame.retval reg.frameptr))]
code (list "rload reg.retaddr (memaddr frame.retaddr reg.frameptr))
code (list "add reg.stackptr reg.frameptr reg.zero)
code (list "rload reg.frameptr (memaddr frame.prevframe reg.stackptr))
code (list "jr reg.retaddr)
mustbe "|;|
end
to arglist
local [token namelist type varflag]
make "varflag "false
ifbe "var [make "varflag "true]
vargroup
foreach :namelist [newarg ? :type :varflag]
ifbeelse "|;| [arglist] [mustbe "|)|]
end
to newarg :pname :type :varflag
if reservedp :pname [(throw "error sentence :pname [reserved word])]
localmake "pointer (list :lexical.depth :framesize)
push "idlist (list :pname :type :pointer :varflag)
make "framesize :framesize + ifelse (and listp :type not :varflag) ~
[arraysize :type] [1]
queue lname :procname ifelse :varflag [list "var :type] [:type]
end
;; Statement part
to blockbody :endword
statement
ifbeelse "|;| [blockbody :endword] [mustbe :endword]
end
to statement
local [token type]
ifbe "begin [compound stop]
ifbe "for [pfor stop]
ifbe "if [pif stop]
ifbe "while [pwhile stop]
ifbe "repeat [prepeat stop]
ifbe "write [pwrite stop]
ifbe "writeln [pwriteln stop]
make "token token
make "peektoken :token
if memberp :token [|;| end until] [stop]
make "type gettype :token
if emptyp :type [(throw "error sentence :token [can't begin statement])]
if equalp :type "procedure [pproccall stop]
if equalp :type "function [pfunset stop]
passign
end
;; Compound statement
to compound
blockbody "end
end
;; Structured statements
to pfor
local [var init step final looptag endtag testreg]
make "var token
mustbe "|:=|
make "init pinteger pexpr
make "step 1
ifbeelse "downto [make "step -1] [mustbe "to]
make "final pinteger pexpr
mustbe "do
make "looptag gensym
make "endtag gensym
code :looptag
localmake "id getid :var
codestore :init (id.pointer :id) (id.varp :id) 0
make "testreg newregister
code (list (ifelse :step<0 ["less] ["gtr]) :testreg :init :final)
code (list "jumpt :testreg (word "" :endtag))
regfree :testreg
statement
code (list "addi :init :init :step)
code (list "jump (word "" :looptag))
code :endtag
regfree :init
regfree :final
end
to prepeat
local [cond looptag]
make "looptag gensym
code :looptag
blockbody "until
make "cond pboolean pexpr
code (list "jumpf :cond (word "" :looptag))
regfree :cond
end
to pif
local [cond elsetag endtag]
make "cond pboolean pexpr
make "elsetag gensym
make "endtag gensym
mustbe "then
code (list "jumpf :cond (word "" :elsetag))
regfree :cond
statement
code (list "jump (word "" :endtag))
code :elsetag
ifbe "else [statement]
code :endtag
end
to pwhile
local [cond looptag endtag]
make "looptag gensym
make "endtag gensym
code :looptag
make "cond pboolean pexpr
code (list "jumpf :cond (word "" :endtag))
regfree :cond
mustbe "do
statement
code (list "jump (word "" :looptag))
code :endtag
end
;; Simple statements: write and writeln
to pwrite
mustbe "|(|
pwrite1
end
to pwrite1
pwrite2
ifbe "|)| [stop]
ifbeelse ", [pwrite1] [(throw "error [missing comma])]
end
to pwrite2
localmake "result pwrite3
ifbe ": [.setfirst (butfirst :result) token]
code :result
if not equalp first :result "putstr [regfree last :result]
end
to pwrite3
localmake "token token
if equalp first :token "' ~
[output (list "putstr 1 (list butlast butfirst :token))]
make "peektoken :token
localmake "result pexpr
if equalp first :result "char [output (list "putch 1 pchar :result)]
if equalp first :result "boolean [output (list "puttf 1 pboolean :result)]
if equalp first :result "integer [output (list "putint 10 pinteger :result)]
output (list "putreal 20 preal :result)
end
to pwriteln
ifbe "|(| [pwrite1]
code [newline]
end
;; Simple statements: procedure call
to pproccall
localmake "pname token
localmake "id getid :pname
localmake "lname id.lname :id
localmake "vartypes thing :lname
pproccall1 framesize.proc
end
to pproccall1 :offset
code (list "store reg.newfp (memaddr frame.save.newfp reg.stackptr))
code (list "add reg.newfp reg.stackptr reg.zero)
code (list "addi reg.stackptr reg.stackptr (last id.frame :id))
code (list "store reg.frameptr (memaddr frame.prevframe reg.newfp))
localmake "newdepth first id.frame :id
ifelse :newdepth > :lexical.depth ~
[code (list "store reg.frameptr
(memaddr frame.outerframe reg.newfp))] ~
[localmake "tempreg newregister
code (list "rload :tempreg (memaddr frame.outerframe reg.frameptr))
repeat (:lexical.depth - :newdepth)
[code (list "rload :tempreg
(memaddr frame.outerframe :tempreg))]
code (list "store :tempreg (memaddr frame.outerframe reg.newfp))
regfree :tempreg]
if not emptyp :vartypes [mustbe "|(| procargs :vartypes :offset]
for [i reg.firstfree :numregs-1] ~
[if item :i :regsused
[code (list "store :i (memaddr frame.regsave+:i reg.frameptr))]]
code (list "add reg.frameptr reg.newfp reg.zero)
code (list "rload reg.newfp (memaddr frame.save.newfp reg.frameptr))
code (list "jal reg.retaddr (word "" :lname))
for [i reg.firstfree :numregs-1] ~
[if item :i :regsused
[code (list "rload :i (memaddr frame.regsave+:i reg.frameptr))]]
end
to procargs :types :offset
if emptyp :types [mustbe "|)| stop]
localmake "next procarg first :types :offset
if not emptyp butfirst :types [mustbe ",]
procargs butfirst :types :offset+:next
end
to procarg :type :offset
local "result
if equalp first :type "var [output procvararg last :type]
if listp :type [output procarrayarg :type]
make "result check.type :type pexpr
code (list "store :result (memaddr :offset reg.newfp))
regfree :result
output 1
end
to procvararg :ftype
local [pname id type index]
make "pname token
make "id getid :pname
make "type id.type :id
ifelse wordp :ftype ~
[setindex "true] ~
[make "index 0]
if not equalp :type :ftype ~
[(throw "error sentence :pname [arg wrong type])]
localmake "target memsetup (id.pointer :id) (id.varp :id) :index
localmake "tempreg newregister
code (list "addi :tempreg (last :target) (first :target))
code (list "store :tempreg (memaddr :offset reg.newfp))
regfree last :target
regfree :tempreg
output 1
end
to procarrayarg :type
localmake "pname token
localmake "id getid :pname
if not equalp :type (id.type :id) ~
[(throw "error (sentence "array :pname [wrong type for arg]))]
localmake "size arraysize :type
localmake "rtarget memsetup (id.pointer :id) (id.varp :id) 0
localmake "pointreg newregister
code (list "addi :pointreg reg.newfp :offset)
localmake "ltarget (list 0 :pointreg)
copyarray
output :size
end
;; Simple statements: assignment statement (including function value)
to passign
local [name id type index value pointer target]
make "name token
make "index []
ifbe "|[| [make "index commalist [pexpr] mustbe "|]|]
mustbe "|:=|
make "id getid :name
make "pointer id.pointer :id
make "type id.type :id
passign1
end
to pfunset
local [name id type index value pointer target]
make "name token
make "index []
if not equalp :name :procname ~
[(throw "error sentence [assign to wrong function] :name)]
mustbe "|:=|
make "pointer (list :lexical.depth frame.retval)
make "type first thing lname :name
make "id (list :name :type :pointer "false)
passign1
end
to passign1
if and (listp :type) (emptyp :index) [parrayassign :id stop]
setindex "false
make "value check.type :type pexpr
codestore :value (id.pointer :id) (id.varp :id) :index
regfree :value
end
to noimmediate :value
if equalp exp.mode :value "immediate ~
[localmake "reg newregister
code (list "addi :reg reg.zero exp.value :value)
output (list exp.type :value "register :reg)]
output :value
end
to check.type :type :result
if equalp :type "real [output preal :result]
if equalp :type "integer [output pinteger :result]
if equalp :type "char [output pchar :result]
if equalp :type "boolean [output pboolean :result]
end
to preal :expr [:pval noimmediate :expr]
if equalp exp.type :pval "real [output exp.value :pval]
output pinteger :pval
end
to pinteger :expr [:pval noimmediate :expr]
local "type
make "type exp.type :pval
if memberp :type [integer boolean char] [output exp.value :pval]
(throw "error sentence exp.type :pval [isn't ordinal])
end
to pchar :expr [:pval noimmediate :expr]
if equalp exp.type :pval "char [output exp.value :pval]
(throw "error sentence exp.type :pval [not character value])
end
to pboolean :expr [:pval noimmediate :expr]
if equalp exp.type :pval "boolean [output exp.value :pval]
(throw "error sentence exp.type :pval [not true or false])
end
to parrayassign :id
localmake "right token
if equalp first :right "' ~
[pstringassign :type (butlast butfirst :right) stop]
localmake "rid getid :right
if not equalp (id.type :id) (id.type :rid) ~
[(throw "error (sentence "arrays :name "and :right [unequal types]))]
localmake "size arraysize id.type :id
localmake "ltarget memsetup (id.pointer :id) (id.varp :id) 0
localmake "rtarget memsetup (id.pointer :rid) (id.varp :rid) 0
copyarray
end
to pstringassign :type :string
if not equalp first :type "char [stringlose]
if not emptyp butfirst last :type [stringlose]
if not equalp (last first last :type) (count :string) [stringlose]
localmake "ltarget memsetup (id.pointer :id) (id.varp :id) 0
pstringassign1 newregister (first :ltarget) (last :ltarget) :string
regfree last :ltarget
end
to pstringassign1 :tempreg :offset :reg :string
if emptyp :string [regfree :tempreg stop]
code (list "addi :tempreg reg.zero ascii first :string)
code (list "store :tempreg (memaddr :offset :reg))
pstringassign1 :tempreg :offset+1 :reg (butfirst :string)
end
to stringlose
(throw "error sentence :name [not string array or wrong size])
end
;; Multiple array indices to linear index computation
to setindex :parseflag
ifelse listp :type ~
[if :parseflag
[mustbe "|[| make "index commalist [pexpr] mustbe "|]| ]
make "index lindex last :type :index
make "type first :type] ~
[make "index 0]
end
to lindex :bounds :index
output lindex1 (offset pinteger noimmediate first :index
first first :bounds) ~
butfirst :bounds butfirst :index
end
to lindex1 :sofar :bounds :index
if emptyp :bounds [output :sofar]
output lindex1 (nextindex :sofar
last first :bounds
pinteger noimmediate first :index
first first :bounds) ~
butfirst :bounds butfirst :index
end
to nextindex :old :factor :new :offset
code (list "muli :old :old :factor)
localmake "newreg offset :new :offset
code (list "add :old :old :newreg)
regfree :newreg
output :old
end
to offset :indexreg :lowbound
if not equalp :lowbound 0 [code (list "subi :indexreg :indexreg :lowbound)]
output :indexreg
end
;; Memory interface: load and store instructions
to codeload :reg :pointer :varflag :index
localmake "target memsetup :pointer :varflag :index
code (list "rload :reg targetaddr)
regfree last :target
end
to codestore :reg :pointer :varflag :index
localmake "target memsetup :pointer :varflag :index
code (list "store :reg targetaddr)
regfree last :target
end
to targetaddr
output memaddr (first :target) (last :target)
end
to memaddr :offset :index
output (word :offset "\( :index "\))
end
to memsetup :pointer :varflag :index
localmake "depth first :pointer
localmake "offset last :pointer
local "newreg
ifelse equalp :depth 0 ~
[make "newreg reg.globalptr] ~
[ifelse equalp :depth :lexical.depth
[make "newreg reg.frameptr]
[make "newreg newregister
code (list "rload :newreg
(memaddr frame.outerframe reg.frameptr))
repeat (:lexical.depth - :depth) - 1
[code (list "rload :newreg
(memaddr frame.outerframe :newreg))]]]
if :varflag ~
[ifelse :newreg = reg.frameptr
[make "newreg newregister
code (list "rload :newreg (memaddr :offset reg.frameptr))]
[code (list "rload :newreg (memaddr :offset :newreg))]
make "offset 0]
if not equalp :index 0 ~
[code (list "add :index :index :newreg)
regfree :newreg
make "newreg :index]
output list :offset :newreg
end
to copyarray
localmake "looptag gensym
localmake "sizereg newregister
code (list "addi :sizereg reg.zero :size)
code :looptag
localmake "tempreg newregister
code (list "rload :tempreg (memaddr (first :rtarget) (last :rtarget)))
code (list "store :tempreg (memaddr (first :ltarget) (last :ltarget)))
code (list "addi (last :rtarget) (last :rtarget) 1)
code (list "addi (last :ltarget) (last :ltarget) 1)
code (list "subi :sizereg :sizereg 1)
code (list "gtr :tempreg :sizereg reg.zero)
code (list "jumpt :tempreg (word "" :looptag))
regfree :sizereg
regfree :tempreg
regfree last :ltarget
regfree last :rtarget
end
;; Expressions
to pexpr
local [opstack datastack parenlevel]
make "opstack [[popen 1 0]]
make "datastack []
make "parenlevel 0
output pexpr1
end
to pexpr1
local [token op]
make "token token
while [equalp :token "|(|] [popen make "token token]
make "op pgetunary :token
if not emptyp :op [output pexprop :op]
push "datastack pdata :token
make "token token
while [and (:parenlevel > 0) (equalp :token "|)| )] ~
[pclose make "token token]
make "op pgetbinary :token
if not emptyp :op [output pexprop :op]
make "peektoken :token
pclose
if not emptyp :opstack [(throw "error [too many operators])]
if not emptyp butfirst :datastack [(throw "error [too many operands])]
output pop "datastack
end
to pexprop :op
while [(op.prec :op) < (1 + op.prec first :opstack)] [ppopop]
push "opstack :op
output pexpr1
end
to popen
push "opstack [popen 1 0]
make "parenlevel :parenlevel + 1
end
to pclose
while [(op.prec first :opstack) > 0] [ppopop]
ignore pop "opstack
make "parenlevel :parenlevel - 1
end
to pgetunary :token
output gprop :token "unary
end
to pgetbinary :token
output gprop :token "binary
end
to ppopop
local [op function args left right type reg]
make "op pop "opstack
make "function op.instr :op
if equalp :function "plus [stop]
make "args op.nargs :op
make "right pop "datastack
make "left (ifelse equalp :args 2 [pop "datastack] [[[] []]])
make "type pnewtype :op exp.type :left exp.type :right
if equalp exp.mode :left "immediate ~
[localmake "leftreg newregister
code (list "addi :leftreg reg.zero exp.value :left)
make "left (list exp.type :left "register :leftreg)]
ifelse equalp exp.mode :left "register ~
[make "reg exp.value :left] ~
[ifelse equalp exp.mode :right "register
[make "reg exp.value :right]
[make "reg newregister]]
if equalp :function "minus ~
[make "left (list exp.type :right "register reg.zero)
make "function "sub
make "args 2]
if equalp exp.mode :right "immediate ~
[make "function word :function "i]
ifelse equalp :args 2 ~
[code (list :function :reg exp.value :left exp.value :right)] ~
[code (list :function :reg exp.value :right)]
if not equalp :reg exp.value :left [regfree exp.value :left]
if (and (equalp exp.mode :right "register)
(not equalp :reg exp.value :right)) ~
[regfree exp.value :right]
push "datastack (list :type "register :reg)
end
to pnewtype :op :ltype :rtype
local "type
make "type op.types :op
if emptyp :ltype [make "ltype :rtype]
if not emptyp last :type [pchecktype last :type :ltype :rtype]
if and (equalp :ltype "real) (equalp :rtype "integer) [make "rtype "real]
if and (equalp :ltype "integer) (equalp :rtype "real) [make "ltype "real]
if not equalp :ltype :rtype [(throw "error [type clash])]
if emptyp last :type ~
[if not memberp :rtype [integer real]
[(throw "error [nonarithmetic type])]]
if emptyp first :type [output :rtype]
output first :type
end
to pchecktype :want :left :right
if not equalp :want :left [(throw "error (sentence :left "isn't :want))]
if not equalp :want :right [(throw "error (sentence :right "isn't :want))]
end
;; Expression elements
to pdata :token
if equalp :token "true [output [boolean immediate 1]]
if equalp :token "false [output [boolean immediate 0]]
if equalp first :token "' [output pchardata :token]
if numberp :token [output (list numtype :token "immediate :token)]
localmake "id getid :token
if emptyp :id [(throw "error sentence [undefined symbol] :token)]
localmake "type id.type :id
if equalp :type "function [output pfuncall :token]
local "index
setindex "true
localmake "reg newregister
codeload :reg (id.pointer :id) (id.varp :id) :index
output (list :type "register :reg)
end
to pchardata :token
if not equalp count :token 3 ~
[(throw "error sentence :token [not single character])]
output (list "char "immediate ascii first butfirst :token)
end
to numtype :number
if memberp ". :number [output "real]
if memberp "e :number [output "real]
output "integer
end
to pfuncall :pname
localmake "id getid :pname
localmake "lname id.lname :id
if namep (word "need :lname) [make (word "need :lname) "true]
localmake "vartypes thing :lname
localmake "returntype first :vartypes
make "vartypes butfirst :vartypes
pproccall1 framesize.fun
localmake "reg newregister
code (list "add :reg reg.retval reg.zero)
output (list :returntype "register :reg)
end
;; Parsing assistance
to code :stuff
if emptyp :stuff [stop]
push :codeinto :stuff
end
to commalist :test [:sofar []]
local [result token]
make "result run :test
if emptyp :result [output :sofar]
ifbe ", [output (commalist :test (lput :result :sofar))]
output lput :result :sofar
end
.macro ifbe :wanted :action
localmake "token token
if equalp :token :wanted [output :action]
make "peektoken :token
output []
end
.macro ifbeelse :wanted :action :else
localmake "token token
if equalp :token :wanted [output :action]
make "peektoken :token
output :else
end
to mustbe :wanted
localmake "token token
if equalp :token :wanted [stop]
(throw "error (sentence "expected :wanted "got :token))
end
to newregister
for [i reg.firstfree :numregs-1] ~
[if not item :i :regsused [setitem :i :regsused "true output :i]]
(throw "error [not enough registers available])
end
to regfree :reg
setitem :reg :regsused "false
end
to reservedp :word
output memberp :word [and array begin case const div do downto else end ~
file for forward function goto if in label mod nil ~
not of packed procedure program record repeat set ~
then to type until var while with]
end
;; Lexical analysis
to token
local [token char]
if namep "peektoken [make "token :peektoken
ern "peektoken output :token]
make "char getchar
if equalp :char "|{| [skipcomment output token]
if equalp :char char 32 [output token]
if equalp :char char 13 [output token]
if equalp :char char 10 [output token]
if equalp :char "' [output string "']
if memberp :char [+ - * / = ( , ) |[| |]| |;|] [output :char]
if equalp :char "|<| [output twochar "|<| [= >]]
if equalp :char "|>| [output twochar "|>| [=]]
if equalp :char ". [output twochar ". [.]]
if equalp :char ": [output twochar ": [=]]
if numberp :char [output number :char]
if letterp ascii :char [output token1 lowercase :char]
(throw "error sentence [unrecognized character:] :char)
end
to skipcomment
if equalp getchar "|}| [stop]
skipcomment
end
to string :string
local "char
make "char getchar
if not equalp :char "' [output string word :string :char]
make "char getchar
if equalp :char "' [output string word :string :char]
make "peekchar :char
output word :string "'
end
to twochar :old :ok
localmake "char getchar
if memberp :char :ok [output word :old :char]
make "peekchar :char
output :old
end
to number :num
local "char
make "char getchar
if equalp :char ". ~
[make "char getchar ~
ifelse equalp :char ". ~
[make "peektoken ".. output :num] ~
[make "peekchar :char output number word :num ".]]
if equalp :char "e [output number word :num twochar "e [+ -]]
if numberp :char [output number word :num :char]
make "peekchar :char
output :num
end
to token1 :token
local "char
make "char getchar
if or letterp ascii :char numberp :char ~
[output token1 word :token lowercase :char]
make "peekchar :char
output :token
end
to letterp :code
if and (:code > 64) (:code < 91) [output "true]
output and (:code > 96) (:code < 123)
end
to getchar
local "char
if namep "peekchar [make "char :peekchar ern "peekchar output :char]
if eofp [output char 1]
output rc1
end
to rc1
local "result
make "result readchar
type :result
output :result
end
;; Data abstraction: ID List
to newlname :word
if memberp :word :namesused [output gensym]
if namep word "% :word [output gensym]
push "namesused :word
output word "% :word
end
to lname :word
local "result
make "result getid :word
if not emptyp :result [output item 3 :result]
(throw "error sentence [unrecognized identifier] :word)
end
to gettype :word
local "result
make "result getid :word
if not emptyp :result [output item 2 :result]
(throw "error sentence [unrecognized identifier] :word)
end
to getid :word [:list :idlist]
if emptyp :list [output []]
if equalp :word first first :list [output first :list]
output (getid :word butfirst :list)
end
to id.type :id
output item 2 :id
end
to id.pointer :id
output item 3 :id
end
to id.lname :id
output item 3 :id
end
to id.varp :id
output item 4 :id
end
to id.frame :id
output item 4 :id
end
;; Data abstraction: Frame slots
to frame.retaddr
output 0
end
to frame.save.newfp
output 1
end
to frame.outerframe
output 2
end
to frame.prevframe
output 3
end
to frame.regsave
output 4
end
to framesize.proc
output 4+:numregs
end
to frame.retval
output 4+:numregs
end
to framesize.fun
output 5+:numregs
end
;; Data abstraction: Operators
to op.instr :op
output first :op
end
to op.nargs :op
output first bf :op
end
to op.types :op
output item 3 :op
end
to op.prec :op
output last :op
end
;; Data abstraction: Expressions
to exp.type :exp
output first :exp
end
to exp.mode :exp
output first butfirst :exp
end
to exp.value :exp
output last :exp
end
;; Data abstraction: Registers
to reg.zero
output 0
end
to reg.retaddr
output 1
end
to reg.stackptr
output 2
end
to reg.globalptr
output 3
end
to reg.frameptr
output 4
end
to reg.newfp
output 5
end
to reg.retval
output 6
end
to reg.firstfree
output 7
end
;; Runtime (machine simulation)
to prun :progname
localmake "prog thing word "% :progname
localmake "regs (array :numregs 0)
local filter "wordp :prog
foreach :prog [if wordp ? [make ? ?rest]]
localmake "memory (array :memsize 0)
setitem 0 :regs 0
if not procedurep "add [runsetup]
prun1 :prog
end
to prun1 :pc
if emptyp :pc [stop]
if listp first :pc [run first :pc]
prun1 butfirst :pc
end
to rload :reg :offset :index
setitem :reg :regs (item (item :index :regs)+:offset :memory)
end
to store :reg :offset :index
setitem (item :index :regs)+:offset :memory (item :reg :regs)
end
to runsetup
foreach [[add sum] [sub difference] [mul product] [quo quotient]
[div [int quotient]] [rem remainder] [land product]
[lor [tobool lessp 0 sum]] [eql [tobool equalp]]
[neq [tobool not equalp]] [less [tobool lessp]]
[gtr [tobool greaterp]] [leq [tobool not greaterp]]
[geq [tobool not lessp]]] ~
[define first ?
`[[dest src1 src2]
[setitem :dest :regs ,@[last ?] (item :src1 :regs)
(item :src2 :regs)]]
define word first ? "i
`[[dest src1 immed]
[setitem :dest :regs ,@[last ?] (item :src1 :regs)
:immed]]]
foreach [[lnot [difference 1]] [sint int] [sround round] [srandom random]] ~
[define first ?
`[[dest src]
[setitem :dest :regs ,@[last ?] (item :src :regs)]]
define word first ? "i
`[[dest immed]
[setitem :dest :regs ,@[last ?] :immed]]]
end
to tobool :tf
output ifelse :tf [1] [0]
end
to jump :label
make "pc fput :label thing :label
end
to jumpt :reg :label
if (item :reg :regs)=1 [jump :label]
end
to jumpf :reg :label
if (item :reg :regs)=0 [jump :label]
end
to jr :reg
make "pc item :reg :regs
end
to jal :reg :label
setitem :reg :regs :pc
jump :label
end
to putch :width :reg
spaces :width 1
type char (item :reg :regs)
end
to putstr :width :string
spaces :width (count first :string)
type :string
end
to puttf :width :bool
spaces :width 1
type ifelse (item :bool :regs)=0 ["F] ["T]
end
to putint :width :reg
localmake "num (item :reg :regs)
spaces :width count :num
type :num
end
to putreal :width :reg
putint :width :reg
end
to spaces :width :count
if :width > :count [repeat :width - :count [type "| |]]
end
to newline
print []
end
to exit
make "pc [exit]
end
Brian Harvey,
bh@cs.berkeley.edu